On Constructing Functions, Part 3
This post is the third example in an ongoing list of various sequences of functions which converge to different things in different ways.
Also in this series:
Example 1: converges almost everywhere but not in $L^1$
Example 2: converges uniformly but not in $L^1$
Example 4: $f_n$ are integrable and converge uniformly to $f$, yet $f$ is not integrable
Example 5: converges pointwise but not in $L^1$
Example 6: converges in $L^1$ but does not converge anywhere

Example 3
A sequence of continuous functions $\{f_n:\mathbb{R}\to[0,\infty)\}$ which converges to 0 in the $L^1$ norm, but does not converge to 0 uniformly.
There are four criteria we want our functions to satisfy:
1. First off is the uniform convergence. Observe that "$\{f_n\}$ does not converge to 0 uniformly" can mean one of three things:
- converges to 0 pointwise only
- converges to something other than 0 (pointwise or uniformly)
- does not converge at all
So it's up to you to decide which one feels more comfortable to work with. Here we'll choose the second option.
2. Next, "$\{f_n\}$ converges to 0 in the $L^1$ norm" means that we want to choose our sequence so that the area under the curve of the $f_n$ gets smaller and smaller as $n\to\infty$.
3. Further, we also want the $f_n$ to be positive (the image of each $f_n$ must be $[0,\infty)$) (notice this allows us to remove the abosolute value sign in the $L^1$ norm: $\int|f_n| \Rightarrow \int f_n$)
4. Lastly, the functions must be continuous.
A slick* but very simple solution is a sequence of triangles of decreasing area with height 1!
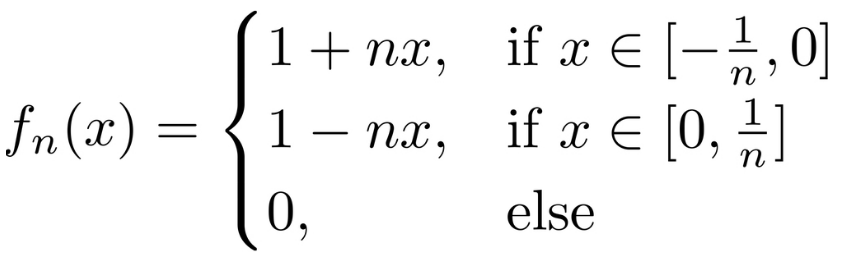
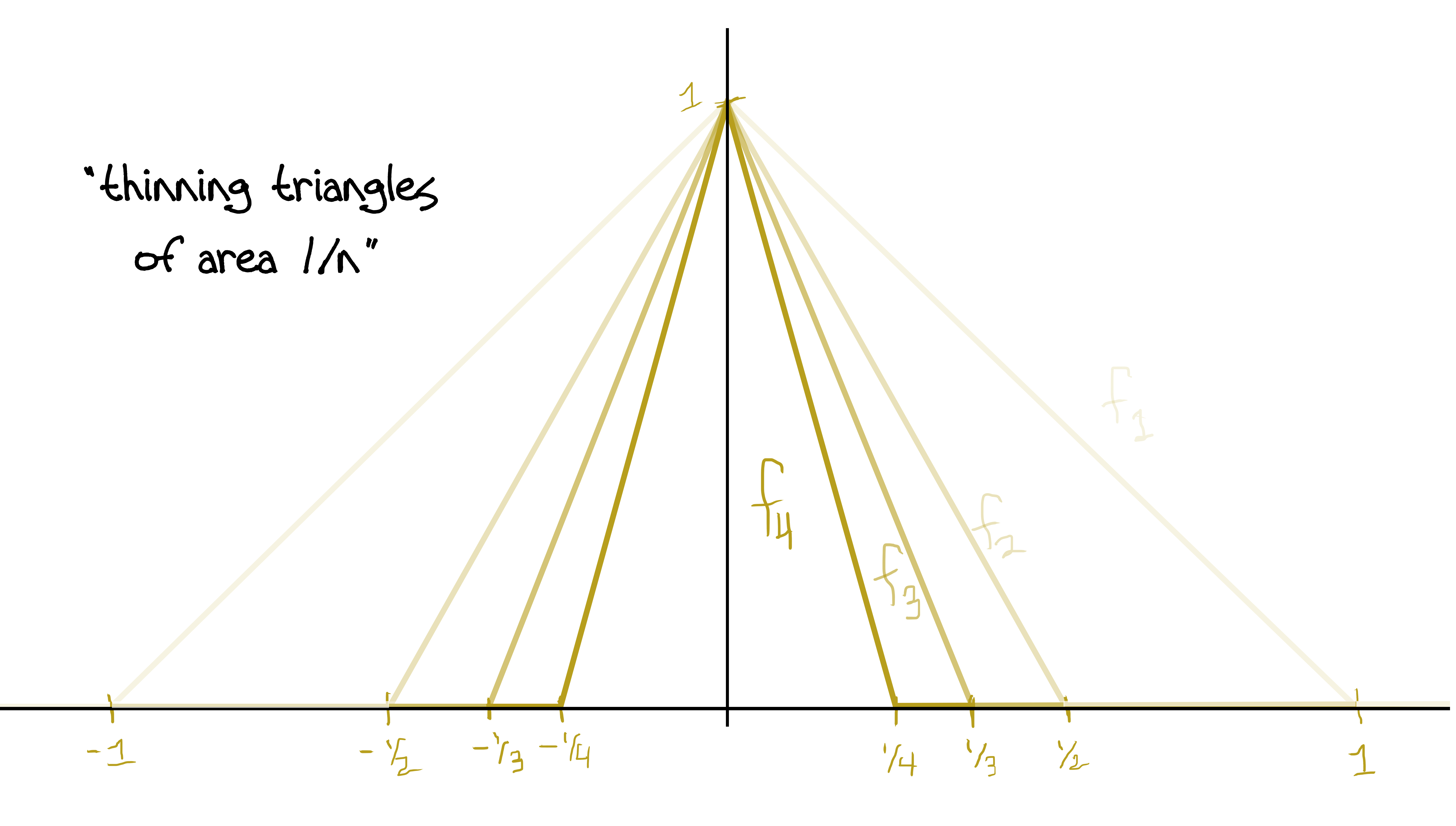
This works because: At $x=0$, $f_n(x)=1$ for all $n$, so there's no way it can converge to zero (much less uniformly). In fact we have $f_n\to f$ pointwise where $$f(x)=\begin{cases} 1, &\text{if $x=0$}\\ 0 &\text{otherwise}. \end{cases}$$ The area of each triangle is $\frac{1}{n}$ which clearly goes to zero for $n$ large. Also, it's clear to see visually that the area is getting smaller. This guarantees $f_n\to 0$ in the $L^1$ norm. Further, each $f_n$ is positive since we've defined it to equal zero as soon as the edges of the triangle reach the $x$-axis. And lastly we have piecewise continuity.
The details: Let $\epsilon>0$ and $x\in \mathbb{R}$. If $x=0$, then $f_n(x)=1$ for all n and so $f_n\to 1$. Otherwise $x>0$ or $x< 0$ If $x>0$ and $x>1$, then $f_n(x)=0$ for all $n$. Otherwise if $x\in(0,1]$ choose $N>\frac{1}{x}$. Then whenever $n>N$ we have $f_n(x)=1-nx< 1-\frac{1}{x}x=0< \epsilon.$ The case when $x< 0$ follows a similar argument.
Lastly $f_n\to 0$ in the $L^1$ norm since, as we mentioned, the areas are decreasing to 0. Explicitly: $$\int_{\mathbb{R}}|f_n| = \int_{-\frac{1}{n}}^0 1+nx + \int_0^{\frac{1}{n}}1-nx = \frac{2}{n}\to 0.$$
*I can brag because this particular example came from a friend. My own attempt at a solution was not nearly as intuitive.
