Hello world! Last summer I wrote a short paper entitled "Entropy as a Topological Operad Derivation," which describes a small but interesting connection between information theory, abstract algebra, and topology. I blogged about it here in June 2021, and the paper was later published in an open-access journal called Entropy in September 2021. In short, it describes a correspondence between Shannon entropy and functions on topological simplices that obey a version of the Leibniz rule from calculus, which I call "derivations of the operad of topological simplices," hence the title.

By what do those words mean? And why is such a theorem interesting?

‍To help make the ideas more accessible, I've recently written a new article aimed at a wide audience to explain it all from the ground up. I'm very excited to share it with you! It's entitled "A New Perspective of Entropy," and a trailer video is below:

As mentioned in the video, the reader is not assumed to have prior familiarity with the words "information theory" or "abstract algebra" or "topology" or even "Shannon entropy." All these ideas are gently introduced from the ground up.

Today I am excited to share that the Math3ma platform has recently grown in a small yet personal way. This new endeavor is in its early stages, but it is one that is close to my heart and gives life to the reasons I started this blog six years ago. A more personal announcement can be found in a new article I wrote for the university, but I'd like to give an update here as well.

This semester I joined The Master's University (TMU), a small private Christian university in southern California, as a visiting research professor of mathematics. I am still a full-time research mathematician in the tech world, but I've also been collaborating part time with the math, science, and engineering faculty at TMU to launch a little research hub on the university's campus and online.

We are calling it The Math3ma Institute, and the website is now live: www.math3ma.institute.

What is The Math3ma Institute?

I've branded our little venture an "institute," though its function is notably different from that of other research institutions. Our vision is that The Math3ma Institute will grow into a place where TMU faculty and advanced undergraduates, along with external colleagues, can engage in research activities in various STEM fields—not just mathematics—and where those results will then be made accessible to a broad audience in easy-to-understand ways. This is summarized in the trifecta boldly displayed on our homepage: discover. share. repeat.

To this end, we are aiming to produce several publicly-available resources, including the launch of semi-annual journal described below.

I recently had the pleasure of chatting with Grant Sanderson on the 3Blue1Brown podcast about a variety of topics, including what first drew me to math and physics, my time in graduate school, thoughts on category theory, basketball, and lots more. We also chatted a bit about Math3ma and its origins, so I thought it'd be fun to share this "behind the scenes" peek with you all here on the blog. Enjoy!

Welcome to the final installment of our mini-series on the new preprint "An Enriched Category Theory of Language," joint work with John Terilla and Yiannis Vlassopoulos. In Part 2 of this series, we discussed a way to assign sets to expressions in language — words like "red" or "blue" – which served as a first approximation to the meanings of those expressions. Motivated by elementary logic, we then found ways to represent combinations of expressions — "red or blue" and "red and blue" and "red implies blue" — using basic constructions from category theory.

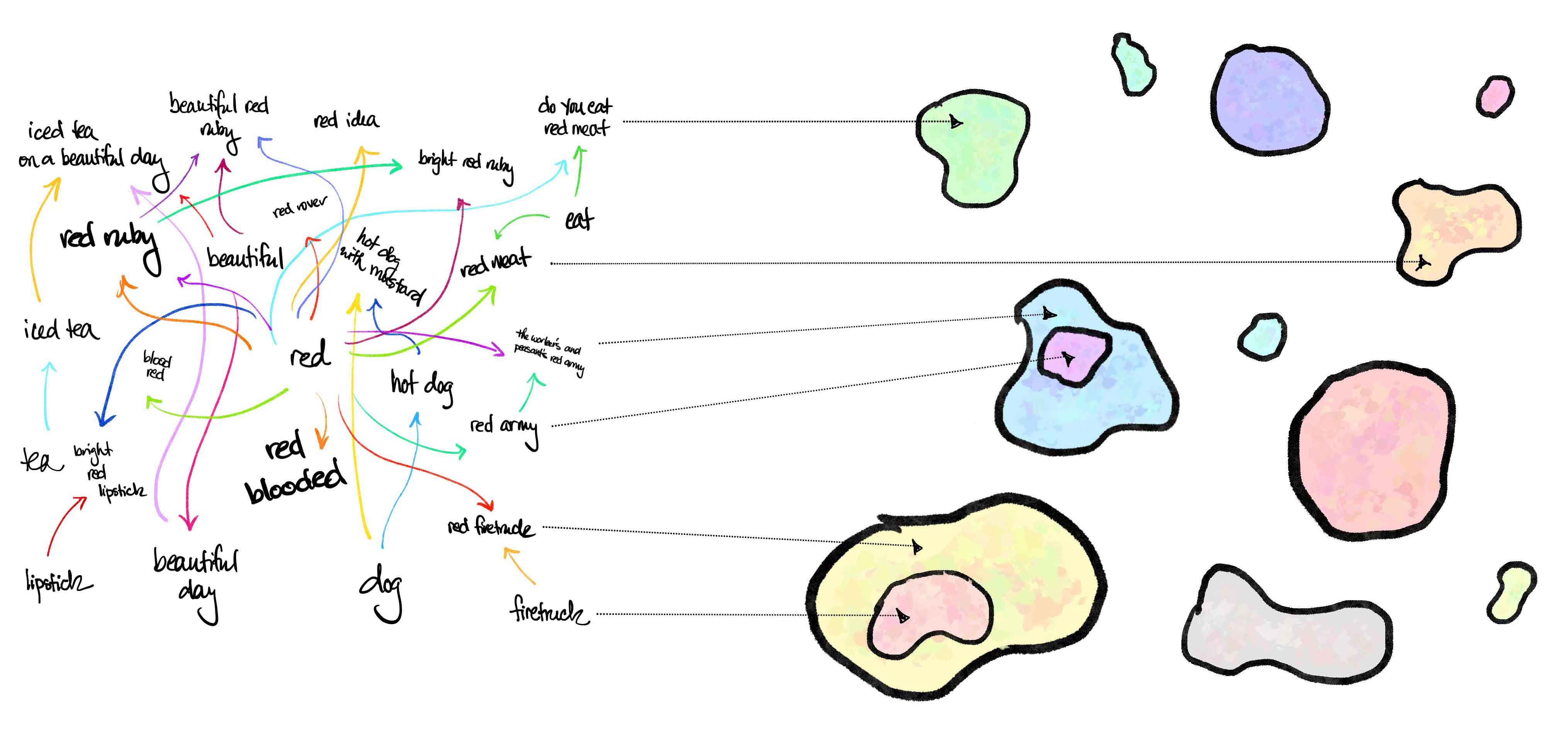
I like to think of Part 2 as a commercial advertising the benefits of a category theoretical approach to language, rather than a merely algebraic one. But as we observed in Part 1, algebraic structure is not all there is to language. There's also statistics! And far from being an afterthought, those statistics play an essential role as evidenced by today's large language models discussed in Part 0.

Happily, category theory already has an established set of tools that allow one to incorporate statistics in a way that's compatible with the considerations of logic discussed last time. In fact, the entire story outlined in Part 2 has a statistical analogue that can be repeated almost verbatim. In today's short post, I'll give lightning-quick summary.

It all begins with a small, yet crucial, twist.

Today I'd like to share a bit of math involving ideas from information theory, algebra, and topology. It's all in a new paper I've recently uploaded to the arXiv, whose abstract you can see on the right. The paper is short — just 11 pages! Even so, I thought it'd be nice to stroll through some of the surrounding mathematics here.

To introduce those ideas, let's start by thinking about the function $d\colon[0,1]\to\mathbb{R}$ defined by $d(x)=-x\log x$ when $x>0$ and $d(x)=0$ when $x=0$. Perhaps after getting out pencil and paper, it's easy to check that this function satisfies an equation that looks a lot like the product rule from Calculus:

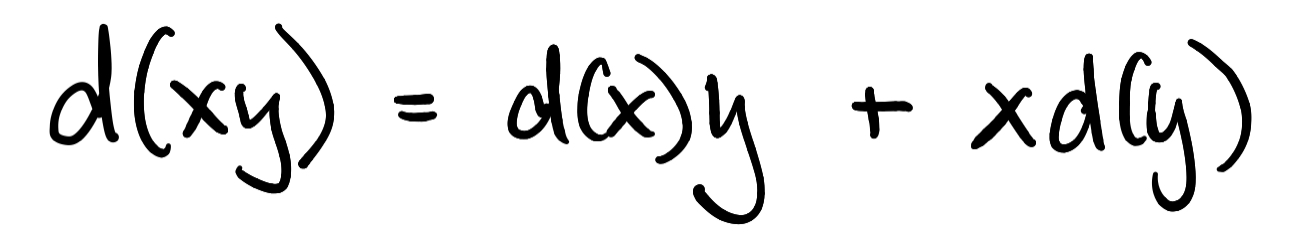
Functions that satisfy an equation reminiscent of the "Leibniz rule," like this one, are called derivations, which invokes the familiar idea of a derivative. The nonzero term $-x\log x$ above may also look familiar to some of you. It's an expression that appears in the Shannon entropy of a probability distribution. A probability distribution on a finite set $\{1,\ldots,n\}$ for $n\geq 1$ is a sequence $p=(p_1,\ldots,p_n)$ of nonnegative real numbers satisfying $\sum_{i=1}^np_i=1$, and the Shannon entropy of $p$ is defined to be

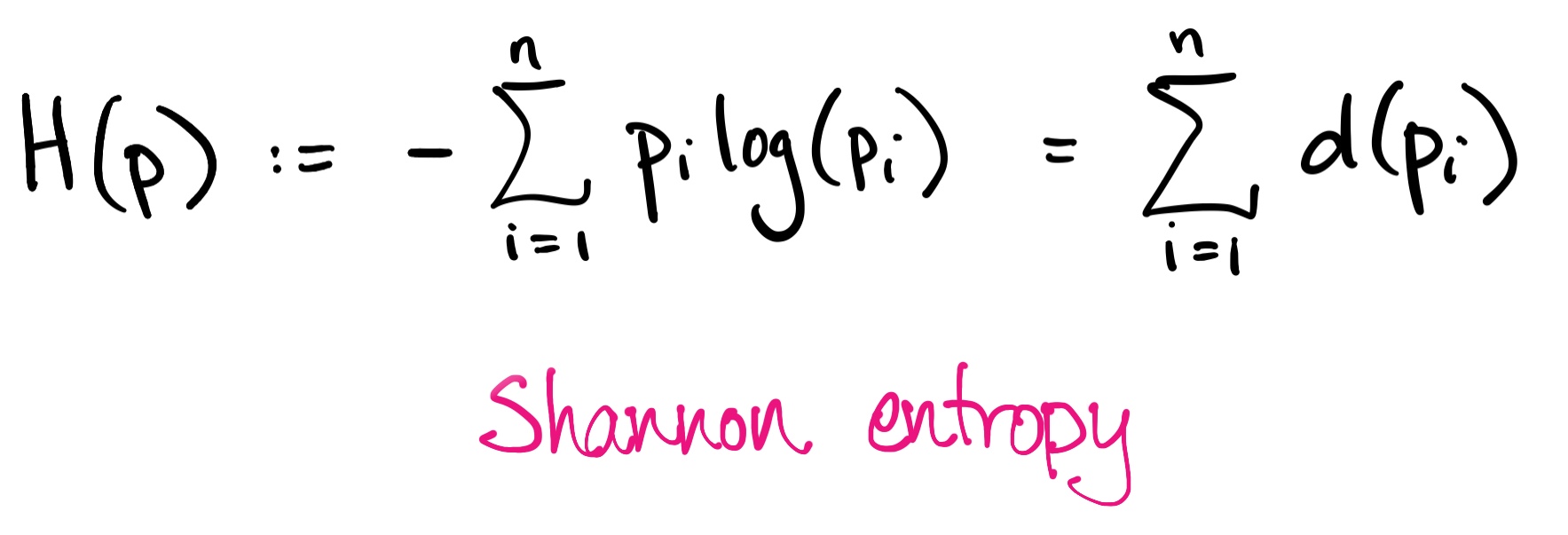
Now it turns out that the function $d$ is nonlinear, which means we can't pull it out in front of the summation. In other words,  $H(p)\neq d(\sum_ip_i).$ Even so, curiosity might cause us to wonder about settings in which Shannon entropy is itself a derivation. One such setting is described in the paper above, which shows a correspondence between Shannon entropy and derivations of (wait for it...) topological simplices!

Part 1 of this mini-series opened with the observation that language is an algebraic structure. But we also mentioned that thinking merely algebraically doesn't get us very far. The algebraic perspective, for instance, is not sufficient to describe the passage from probability distributions on corpora of text to syntactic and semantic information in language that wee see in today's large language models. This motivated the category theoretical framework presented in a new paper I shared last time. But even before we bring statistics into the picture, there are some immediate advantages to using tools from category theory rather than algebra. One example comes from elementary considerations of logic, and that's where we'll pick up today.

Let's start with a brief recap.

In the previous post I mentioned a new preprint that John Terilla, Yiannis Vlassopoulos, and I recently posted on the arXiv. In it, we ask a question motivated by the recent successes of the world's best large language models:

What's a nice mathematical framework in which to explain the passage from probability distributions on text to syntactic and semantic information in language?

To understand the motivation behind this question, and to recall what a "large language model" is, I'll encourage you to read the opening article from last time. In the next few blog posts, I'll give a tour of mathematical ideas presented in the paper towards answering the question above. I like the narrative we give, so I'll follow it closely here on the blog. You might think of the next few posts as an informal tour through the formal ideas found in the paper.

Now, where shall we begin? What math are we talking about?

Let's start with a simple fact about language.

Language is algebraic.

By "algebraic," I mean the basic sense in which things combine to form a new thing. We learn about algebra at a young age: given two numbers $x$ and $y$ we can multiply them to get a new number $xy$. We can do something similar in language. Numbers combine to give new numbers, and words and phrases in a language combine to give new expressions. Take the words red and firetruck, for example. They can be "multiplied" together to get a new phrase: red firetruck.

Here, the "multiplication" is just concatenation — sticking things side by side. This is a simple algebraic structure, and it's inherent to language. I'm concatenating words together as I type this sentence. That's algebra! Another word for this kind of structure is compositionality, where things compose together to form something larger.

So language is algebraic or compositional.

What is applied mathematics? The phrase might bring to mind historical applications of analysis to physical problems, or something similar. I think that's often what folks mean when they say "applied mathematics." And yet there's a much broader sense in which mathematics is applied, especially nowadays. I like what mathematician Tom Leinster once had to say about this (emphasis mine):

"I hope mathematicians and other scientists hurry up and realize that there’s a glittering array of applications of mathematics in which non-traditional areas of mathematics are applied to non-traditional problems. It does no one any favours to keep using the term 'applied mathematics' in its current overly narrow sense."

I'm all in favor of rebranding the term "applied mathematics" to encompass this wider notion. I certainly enjoy applying non-traditional areas of mathematics to non-traditional problems — it's such a vibrant place to be! It's especially fun to take ideas that mathematicians already know lots about, then repurpose those ideas for potential applications in other domains. In fact, I plan to spend some time sharing one such example with you here on the blog.

But before sharing the math— which I'll do in the next couple of blog posts — I want to first motivate the story by telling you about an idea from the field of artificial intelligence (AI).

‍

The TensorFlow channel on YouTube recently uploaded a video I made on some elementary ideas from linear algebra and how they're used in machine learning (ML). It's a very nontechnical introduction — more of a bird's-eye view of some basic concepts and standard applications — with the simple goal of whetting the viewer's appetite to learn more.

I've decided to share it here, too, in case it may be of interest to anyone!

I imagine the content here might be helpful for undergraduate students who are in their first exposure to linear algebra and/or to ML, or for anyone else who's new to the topic and wants to get an idea for what it is and some ways it's used.

The video covers three basic concepts — vectors and matrix factorizations and eigenvectors/eigenvalues — and explains a few ways these concepts arise in ML — namely, as data representations, to find vector embeddings, and for dimensionality reduction techniques, respectively.

Enjoy!

Let's jump right in to where we left off in part 1 of our warm-up to enriched category theory. If you'll recall from last time, we saw that the set of truth values $\{0, 1\}$ and the unit interval $[0,1]$ and the nonnegative extended reals $[0,\infty]$ were not just sets but actually preorders and hence categories. We also hinted at the idea that a "category enriched over" one of these preorders (whatever that means — we hadn't defined it yet!) looks something like a collection of objects $X,Y,\ldots$ where there is at most one arrow between any pair $X$ and $Y$, and where that arrow can further be "decorated with" —or simply replaced by — a number from one of those three exemplary preorders.

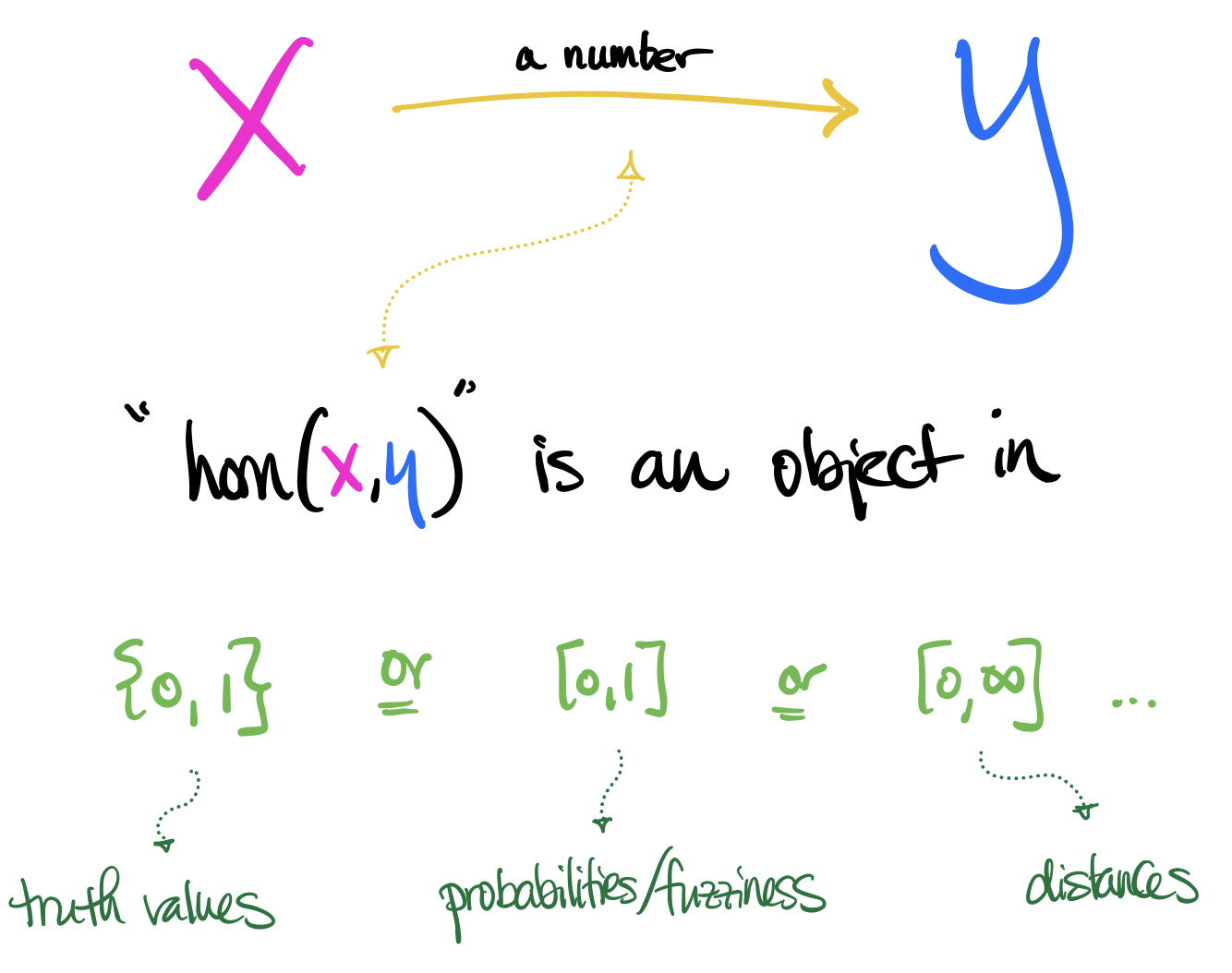
With that background in mind, my goal in today's article is to say exactly what a category enriched over a preorder is. The formal definition — and the intuition behind it — will then pave the way for the notion of a category enriched over an arbitrary (and sufficiently nice) category, not just a preorder.

En route to this goal, it will help to make a couple of opening remarks.

Two things to think about.

First, take a closer look at the picture on the right. I've written "$\text{hom}(X,Y)$" in quotation marks because the notation $\text{hom}(-,-)$ is often used for a set of morphisms in ordinary category theory. But the  point of this discussion is that we're not just interested in sets! So we should use better notation: let's refer to the number associated to a pair of objects $XY$ and $Y$ as $\mathcal{C}(X,Y)$, where the letter "$\mathcal{C}$" reminds us there's an (enriched) $\mathcal{C}$ategory being investigated.

Second, for the theory to work out nicely, it turns out that preorders need a little more added to them.

It's no secret that I like category theory. It's a common theme on this blog, and it provides a nice lens through which to view old ideas in new ways — and to view new ideas in new ways! Speaking of new ideas, my coauthors and I are planning to upload a new paper on the arXiv soon. I've really enjoyed the work and can't wait to share it with you. But first, you'll have to know a little something about enriched category theory. (And before that, you'll have to know something about ordinary category theory... here's an intro!) So that's what I'd like to introduce today.

A warm up, if you will.

What is enriched category theory?

As the name suggests, it's like a "richer" version of category theory, and it all starts with a simple observation. (Get your category theory hats on, people. We're jumping right in!)

In a category, you have some objects and some arrows between them, thought of as relationships between those objects. Now in the formal definition of a category, we usually ask for a set's worth of morphisms between any two objects, say $X$ and $Y$. You'll typically hear something like, "The hom set $\text{hom}(X,Y)$ bla bla...."
‍

Now here's the thing. Quite often in mathematics, the set $\text{hom}(X,Y)$ may not just be a set. It could, for instance, be a set equipped with extra structure. You already know lots of examples. Let's think about about linear algebra, for a moment.

Over the years, the articles on this blog have spanned a wide range of audiences, from fun facts (Multiplying Non-Numbers), to undergraduate level (The First Isomorphism Theorem, Intuitively), to graduate level (What is an Operad?), to research level. Today's article is more on the fun-fact side of things, along with—like most articles here—an eye towards category theory.

So here's a fun fact about greatest common divisors (GCDs) and the Fibonacci sequence $F_1,F_2,F_3,\ldots$, where $F_1=F_2=1$ and $F_n:=F_{n-1} + F_{n-2}$ for $n>1$. For all $n,m\geq 1$,

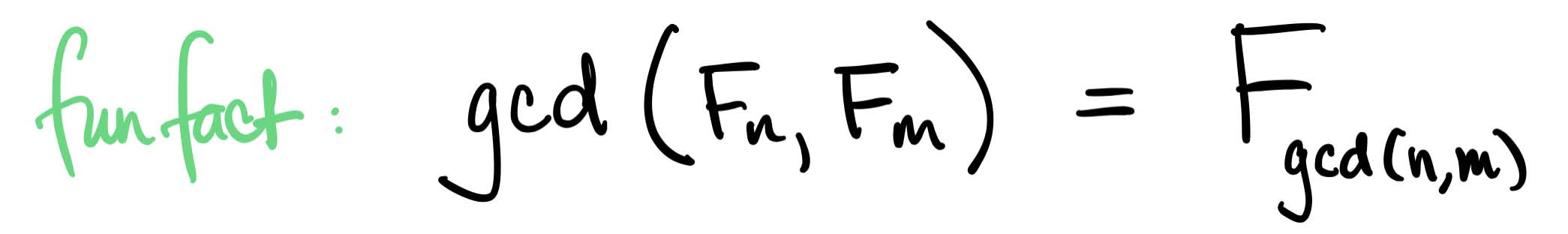
In words, the greatest common divisor of the $n$th and $m$th Fibonacci numbers is the Fibonacci number whose index is the greatest common divisor of $n$ and $m$. (Here's a proof.) Upon seeing this, your "spidey senses" might be tingling. Surely there's some structure-preserving map $F$ lurking in the background, and this identity means it has a certain nice property. But what is that map? And what structure does it preserve? And what's the formal way to describe the nice property it has?

The short answer is that the natural numbers $\mathbb{N}=\{1,2,3,\ldots\}$ form a partially ordered set (poset) under division, and the function $F\colon \mathbb{N}\to\mathbb{N}$ defined by $n\mapsto F_n:=F(n)$ preserves meets: $F_n\wedge F_m = F(n\wedge m)$.

Quantum entanglement is, as you know, a phrase that's jam-packed with meaning in physics. But what you might not know is that the linear algebra behind it is quite simple. If you're familiar with singular value decomposition (SVD), then you're 99% there. My goal for this post is to close that 1% gap. In particular, I'd like to explain something called the Schmidt rank in the hopes of helping the math of entanglement feel a little less... tangly. And to do so, I'll ask that you momentarily forget about the previous sentences. Temporarily ignore the title of this article. Forget we're having a discussion about entanglement. Forget I mentioned that word. And let's start over. Let's just chat math.

Let's talk about SVD.

Singular Value Decomposition

SVD is arguably one of the most important, well-known tools in linear algebra. You are likely already very familiar with it, but here's a lightening-fast recap. Every matrix $M$ can be factored as $M=UDV^\dagger$ as shown below, called the singular value decomposition of $M$. The entries of the diagonal matrix $D$ are nonnegative numbers called singular values, and the number of them is equal to the rank of $M$, say $k$. What's more, $U$ and $V$ have exactly $k$ columns, called the left and right singular vectors, respectively.

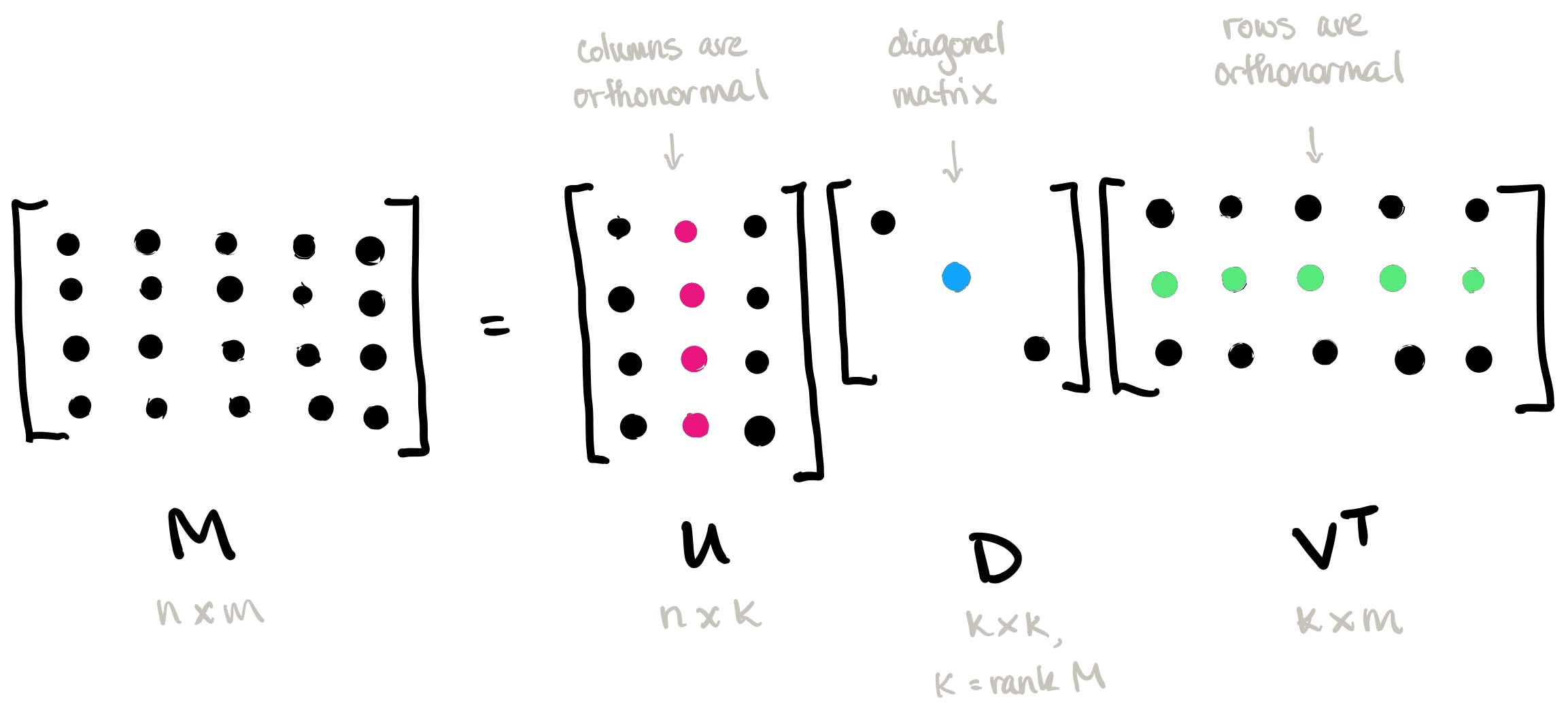
There are different ways to think about this, depending on which applications you have in mind. I like to think of singular vectors as encoding meaningful "concepts" inherent to $M$, and of singular values as indicating how important those concepts are.

This is the official launch week of our new book, Topology: A Categorical Approach, which is now available for purchase! We're also happy to offer a free open access version through MIT Press at topology.mitpress.mit.edu.

Inside, you'll find a presentation of basic, point-set topology from the perspective of category theory, targeted at graduate students in a first-semester course on topology. The idea is that most of these students are already somewhat familiar with the point-set ideas through a course on analysis or undergraduate topology. For this reason, many graduate-level instructors are tempted to rush through point-set topology or to skip it altogether to reach algebraic topology, which can be more fun to learn and to teach.

Our book presents an alternative to this approach. Rather than skipping over the basic ideas, we view this as an excellent opportunity to introduce students to the modern viewpoint of category theory. 

Today I'd like to share with you a new paper on the arXiv—my latest project in collaboration with mathematician Yiannis Vlassopoulos (Tunnel, IHES). To whet your appetite, let me first set the stage. A few months ago I made a 10-minute introductory video to my PhD thesis, which was an investigation into mathematical structure that is both algebraic and statistical. In the video, I noted that natural language is an example of where such mathematical structure can be found.

Language is algebraic, since words can be concatenated to form longer expressions.  Language is also statistical, since some expressions occur more frequently than others.

As a simple example, take the words "orange" and "fruit." We can stick them together to get a new phrase, "orange fruit." Or we could put "orange" together with "idea" to get "orange idea." That might sound silly to us, since the phrase "orange idea" occurs less frequently in English than "orange fruit." But that's the point. These frequencies contribute something to the meanings of these expressions. So what is this kind of mathematical structure? As I mention in the video, it's helpful to have a set of tools to start exploring it, and basic ideas from quantum physics are one source of inspiration. I won't get into this now—you can watch the video or read the thesis! But I do want to emphasize the following: In certain contexts, these tools provide a way to see that statistics can serve as a proxy for meaning. I didn't explain how in the video. I left it as a cliffhanger.

But I'll tell you the rest of the story now.

Before introducing today's post, I'd like to first thank everyone who's reached out to me about my thesis and video posted last week. Thanks! I appreciate all the generous feedback. Now onto the topic of the day: I'd like to share an update about what's coming next, both for me and for the blog.

First, a word on the blog.

What's next for Math3ma?

I created Math3ma in early 2015 as an aid in transitioning from undergraduate-level to graduate-level mathematics. And it worked! The blog has been a sort of public math journal for more than five years, and I'm so glad I started it. My appreciation extends to all readers and to everyone who has contacted me through the site over the years. I'm always delighted to hear that the blog has been helpful for you, as well.

So since Math3ma has accomplished its purpose, my use for it will change. As you may have noticed already, I blog less frequently than I used to, and the content of my more recent articles is slightly different than the content in 2015--2017.

So what will happen to Math3ma going forward? I don't know, and I plan to be flexible about this. Of course I'll leave the website up, but going forward I plan to be flexible with how often I'll blog (not often, probably) and with what I'll blog about (my research, probably). I don't have any big plans for upcoming blog posts, so I may just take a break for a while. On the other hand, I do plan to post a paper or two on the arXiv in the near future, and I might decide to blog about it since I find sharing math irresistible.

See? Flexible.

I'm happy to share that I've successfully defended my PhD thesis, and my dissertation—"At the Interface of Algebra and Statistics"—is now available online at arXiv:2004.05631. In a few words,

my thesis uses basic tools from quantum physics to investigate mathematical structure that is both algebraic and statistical.

What do I mean? Well, the dissertation is about 130 pages long, which I realize is a lot to chew. So I made a 10-minute introductory video! It gives a brief tour of the paper and describes what I think is the quickest way to get a feel for what's inside.

Now, let me highlight an important point that I make in the video:

I wrote my dissertation with a wide audience in mind.

In particular, there is a great deal of exposition woven into the mathematics that provides intuition and motivation for the ideas. I’ve also sprinkled several “behind the scenes” snippets throughout, and alongside the propositions, lemmas, and corollaries there are Takeaways that summarize key ideas. Several of these key ideas are introduced through simple examples that are placed before—not after—the theory they're meant to illustrate. And in a happy turn of events, there is a low entrance fee for following the mathematics. The main tools are linear algebra and basic probability theory. And yes, there is some category theory, too!

I've been collaborating on an exciting project for quite some time now, and today I'm happy to share it with you. There is a new topology book on the market! Topology: A Categorical Approach is a graduate-level textbook that presents basic topology from the modern perspective of category theory. Coauthored with Tyler Bryson and John Terilla, Topology is published through MIT Press and will be released on August 18, 2020. But you can pre-order on Amazon now! 

Here is the book's official description:

This graduate-level textbook on topology takes a unique approach: it reintroduces basic, point-set topology from a more modern, categorical perspective. Many graduate students are familiar with the ideas of point-set topology and they are ready to learn something new about them. Teaching the subject using category theory—a contemporary branch of mathematics that provides a way to represent abstract concepts—both deepens students' understanding of elementary topology and lays a solid foundation for future work in advanced topics.

After presenting the basics of both category theory and topology, the book covers the universal properties of familiar constructions and three main topological properties—connectedness, Hausdorff, and compactness. It presents a fine-grained approach to convergence of sequences and filters; explores categorical limits and colimits, with examples; looks in detail at adjunctions in topology, particularly in mapping spaces; and examines additional adjunctions, presenting ideas from homotopy theory, the fundamental groupoid, and the Seifert van Kampen theorem. End-of-chapter exercises allow students to apply what they have learned. The book expertly guides students of topology through the important transition from undergraduate student with a solid background in analysis or point-set topology to graduate student preparing to work on contemporary problems in mathematics.

Hi all, just ducking in to help spread the word: the annual applied category theory conference (ACT2020) is taking place remotely this summer! Be sure to check out the conference website for the latest updates.

As you might know, I was around for ACT2018, which inspired my What is Applied Category Theory? booklet. This year I'm on the program committee and plan to be around for the main conference in July. Speaking of, here are the dates to know:

• Adjoint School: June 29 -- July 3
• Tutorial Day: July 5
• Main Conference: July 6 -- 10

The Adjoint School is a months-long online reading group, where participants paired with researchers work through some of the major papers in the field. It culminates in an in-person meet-up a week before the main conference. Unfortunately, the deadline apply to the school is already closed. But this year, the conference has a Tutorial Day, too! I love this idea. It's open to anyone (first-come first serve) who's new to applied category theory and wants a little more background to get the most out of the talks during the main conference. You'll get to meet with Paolo Perrone, David Spivak, and Emily Riehl and learn math! And here's a quick blurb about the main conference, taken from this year's website.

How far along are you in graduate school? What exactly is it that you do? These are two questions I'm asked frequently these days and am happy to answer. I created Math3ma precisely for my time in graduate school, so I thought it'd be appropriate to share the answers here, too, as a quick update! First,

I'm graduating this semester!

It's exciting. I've really enjoyed my time as a graduate student and have been looking forward to the future for a while now. (I'll share more on my post-graduate plans in another post.) In the mean time, I'm in the midst of writing up my dissertation. The title is pending. Stay tuned!

Now to the second question: "What's your research about anyways?"

My work doesn't fit into any one mathematical label (geometry, topology, algebra, category theory, etc.), so it's hard to answer this question with just one or two words. I'm using different ideas to make connections across different things! And I love it for that reason. I'll elaborate.

I'm in pure mathematics program, but some of the most exciting mathematics is, to me personally, that which is inspired by cross-discipline communication. I am most deeply moved by mathematics that is motivated by some phenomena in nature, or in physics, or in an applied setting.

Amazingly, my thesis is in this very space! (Just three years ago, I didn't know I'd be doing what I'm doing now, hence "amazingly." It's a very cool story, but I'll save it for another day.)

In the past few months, I've shared a few mathematical ideas that I think are pretty neat: drawing matrices as bipartite graphs, picturing linear maps as tensor network diagrams, and understanding the linear algebraic (or "quantum") versions of probabilities.‍

These ideas are all related by a project I've been working on with Miles Stoudenmire—a research scientist at the Flatiron Institute—and John Terilla—a mathematician at CUNY and Tunnel. We recently posted a paper on the arXiv: "Modeling sequences with quantum states: a look under the hood," and today I'd like to tell you a little about it.

‍

Welcome to the last installment in our mini-series on adjunctions in category theory. We motivated the discussion in Part 1 and walked through formal definitions in Part 2. Today I'll share some examples. In Mac Lane's well-known words, "adjoint functors arise everywhere," so this post contains only a tiny subset of examples. Even so, I hope they'll help give you an eye for adjunctions and enhance your vision to spot them elsewhere.

An adjunction, you'll recall, consists of a pair of functors $F\dashv G$ between categories $\mathsf{C}$ and $\mathsf{D}$ together with a bijection of sets, as below, for all objects $X$ in $\mathsf{C}$ and $Y$ in $\mathsf{D}$.

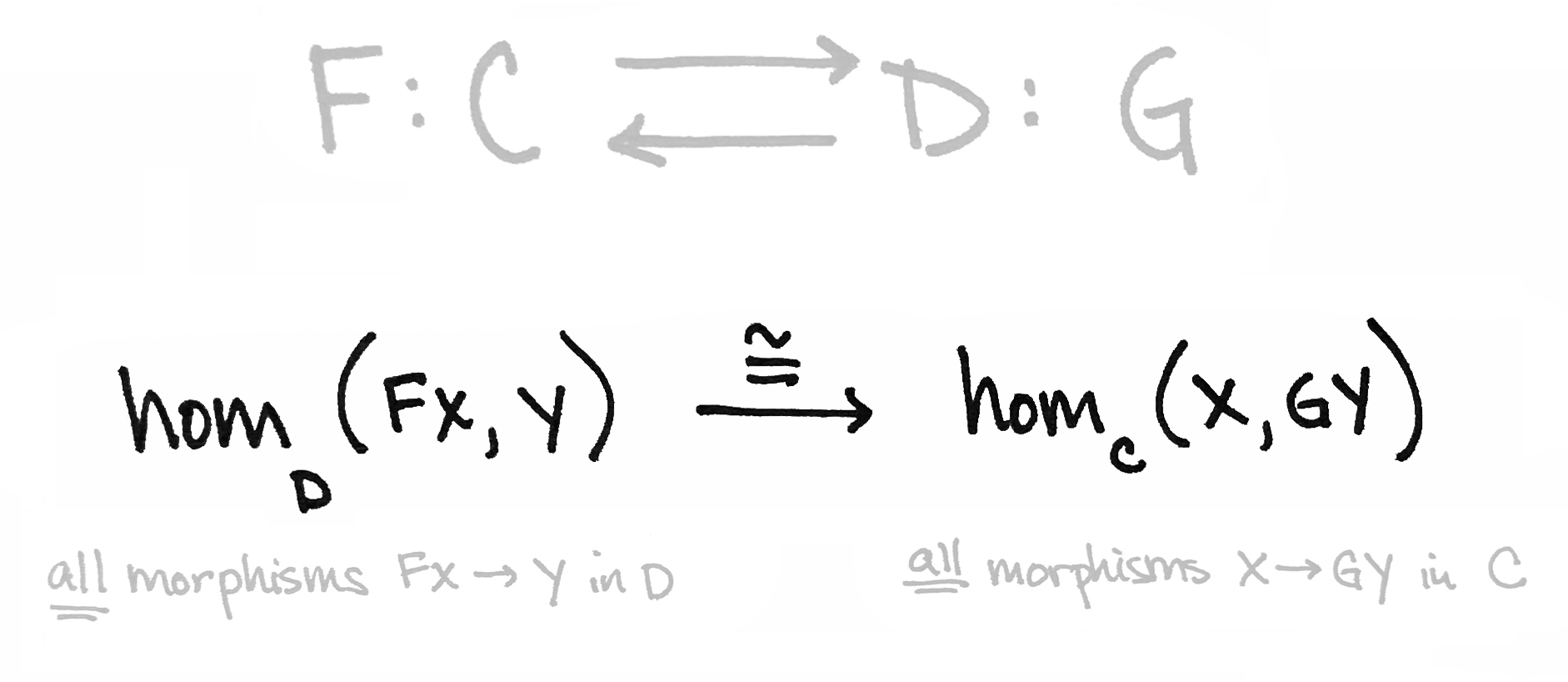
In Part 2, we illustrated this bijection using a free-forgetful adjunction in linear algebra as our guide. So let's put "free-forgetful adjuctions" first on today's list of examples.

Last time I shared a light introduction to adjunctions in category theory. As we saw then, an adjunction consists of a pair of opposing functors $F$ and $G$ together with natural transformations $\text{id}\to\ GF$ and $FG\to\text{id}$. We compared this to two stricter scenarios: one where the composite functors equal the identities, and one where they are naturally isomorphic to the identities. The first scenario defines an isomorphism of categories. The second defines an equivalence of categories. An adjunction is third on the list.

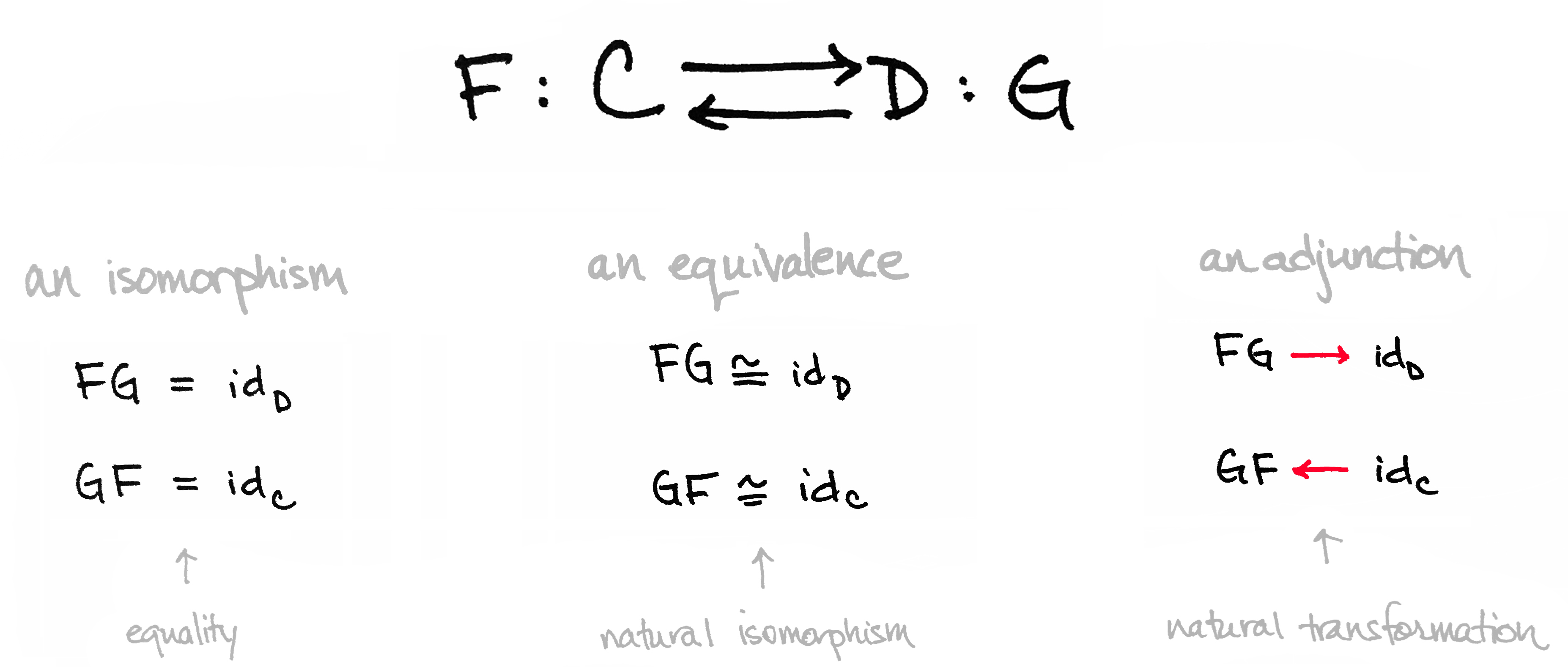
In the case of an adjunction, we also ask that the natural transformations—called the unit and counit—somewhat behave as inverses of each other. This explains why the ${\color{red}\text{arrows}}$ point in opposite directions. (It also explains the "co.") Except, they can't literally be inverses since they're not composable: one involves morphisms in $\mathsf{C}$ and the other involves morphisms in $\mathsf{D}$. That is, their (co)domains don't match. But we can fix this by applying $F$ and $G$ so that (a modified version of) the unit and counit can indeed be composed. This brings us to the formal definition of an adjunction.

Some time ago, I started a "What is...?" series introducing the basics of category theory:

• "What is a category?"
• "What is a functor?" Part 1 and Part 2
• "What is a natural transformation?" Part 1 and Part 2

Today, we'll add adjunctions to the list. An adjunction is a pair of functors that interact in a particularly nice way. There's more to it, of course, so I'd like to share some motivation first. And rather than squeezing the motivation, the formal definition, and some examples into a single post, it will be good to take our time: Today, the motivation. Next time, the formal definition. Afterwards, I'll share examples.

Indeed, I will make the admittedly provocative claim that adjointness is a concept of fundamental logical and mathematical importance that is not captured elsewhere in mathematics.

- Steve Awodey (in Category Theory, Oxford Logic Guides)

Welcome back to our mini-series on quantum probability! Last time, we motivated the series by pondering over a thought from classical probability theory, namely that marginal probability doesn't have memory. That is, the process of summing over of a variable in a joint probability distribution causes information about that variable to be lost. But as we saw then, there is a quantum version of marginal probability that behaves much like "marginal probability with memory." It remembers what's destroyed when computing marginals in the usual way. In today's post, I'll unveil the details. Along the way, we'll take an introductory look at the mathematics of quantum probability theory.

Let's begin with a brief recap of the ideas covered in Part 1: We began with a joint probability distribution on a product of finite sets $p\colon X\times Y\to [0,1]$ and realized it as a matrix $M$ by setting $M_{ij} = \sqrt{p(x_i),p(y_j)}$. We called elements of our set $X=\{0,1\}$ prefixes and the elements of our set $Y=\{00,11,01,10\}$ suffixes so that $X\times Y$ is the set of all bitstrings of length 3.

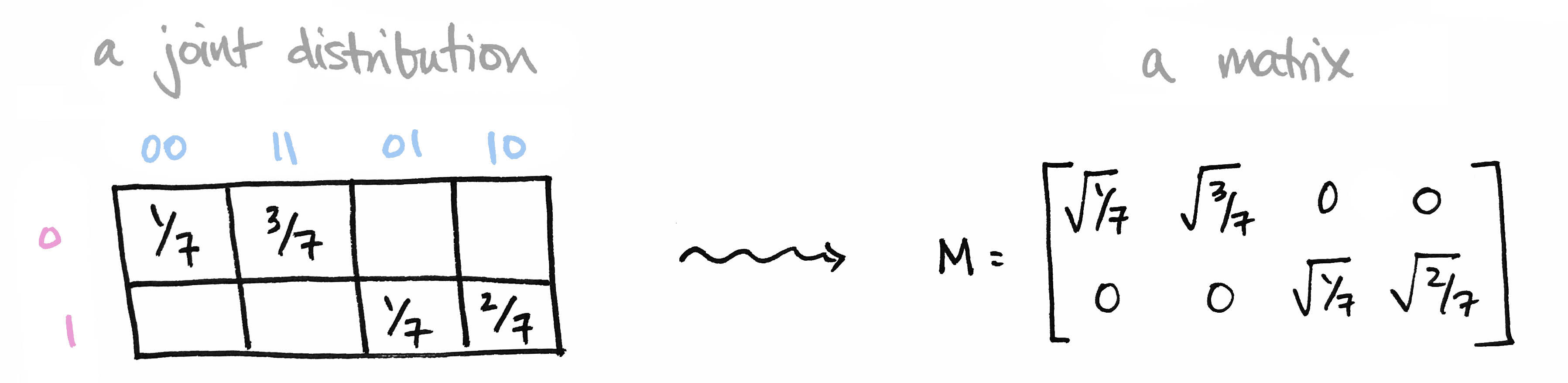
We then observed that the matrix $M^\top M$ contains the marginal probability distribution of $Y$ along its diagonal. Moreover its eigenvectors define conditional probability distributions on $Y$. Likewise, $MM^\top$ contains marginals on $X$ along its diagonal, and its eigenvectors define conditional probability distributions on $X$.

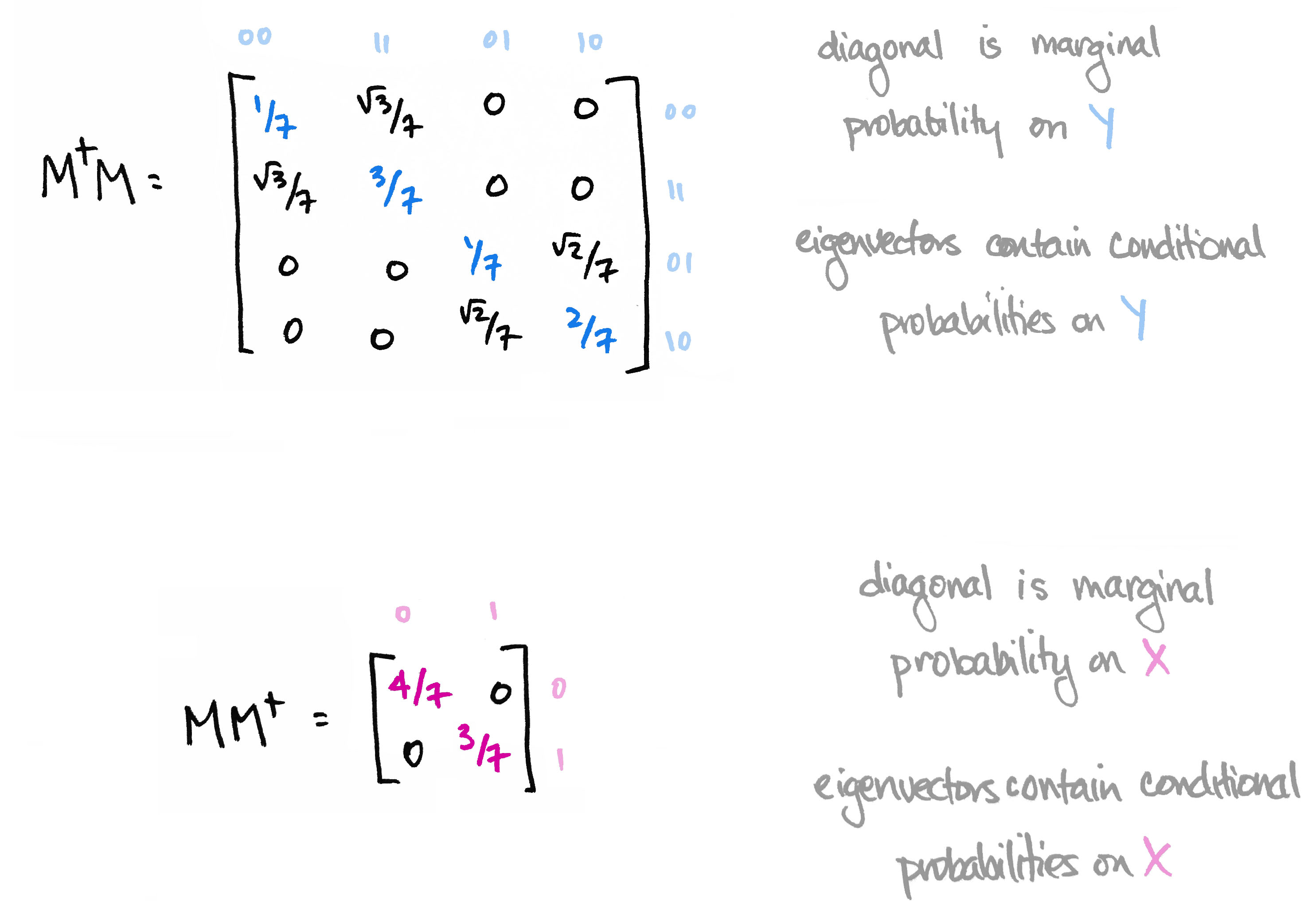
The information in the eigenvectors of $M^\top M$ and $MM^\top$ is precisely the information that's  destroyed when computing marginal probability in the usual way. The big reveal last time was that the matrices $M^\top M$ and $MM^\top$ are the quantum versions of marginal probability distributions.

As we'll see today, the quantum version of a probability distribution is something called a density operator. The quantum version of marginalizing corresponds to "reducing" that operator to a subsystem. This reduction is a construction in linear algebra called the partial trace. I'll start off by explaining the partial trace. Then I'll introduce the basics of quantum probability theory. At the end, we'll tie it all back to our bitstring example.

In this article and the next, I'd like to share some ideas from the world of quantum probability.* The word "quantum" is pretty loaded, but don't let that scare you. We'll take a first—not second or third—look at the subject, and the only prerequisites will be linear algebra and basic probability. In fact, I like to think of quantum probability as another name for "linear algebra + probability," so this mini-series will explore the mathematics, rather than the physics, of the subject.**

In today's post, we'll motivate the discussion by saying a few words about (classical) probability. In particular, let's spend a few moments thinking about the following: ‍

What do I mean? We'll start with some basic definitions. Then I'll share an example that illustrates this idea.

A probability distribution (or simply, distribution) on a finite set $X$ is a function $p \colon X\to [0,1]$ satisfying $\sum_x p(x) = 1$. I'll use the term joint probability distribution to refer to a distribution on a Cartesian product of finite sets, i.e. a function $p\colon X\times Y\to [0,1]$ satisfying $\sum_{(x,y)}p(x,y)=1$. Every joint distribution defines a marginal probability distribution on one of the sets by summing probabilities over the other set. For instance, the marginal distribution $p_X\colon X\to [0,1]$ on $X$ is defined by $p_X(x)=\sum_yp(x,y)$, in which the variable $y$ is summed, or "integrated," out. It's this very process of summing or integrating out that causes information to be lost. In other words, marginalizing loses information. It doesn't remember what was summed away!

I'll illustrate this with a simple example. To do so, I need to give you some finite sets $X$ and $Y$ and a probability distribution on them.

In the previous post, I described a simple way to think about matrices, namely as bipartite graphs. Today I'd like to share a different way to picture matrices—one which is used not only in mathematics, but also in physics and machine learning. Here's the basic idea. An $m\times n$ matrix $M$ with real entries represents a linear map from $\mathbb{R}^n\to\mathbb{R}^m$. Such a mapping can be pictured as a node with two edges. One edge represents the input space, the other edge represents the output space.

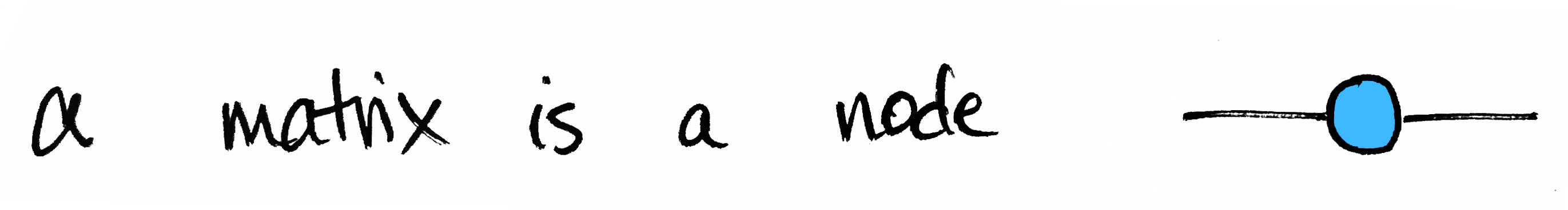
That's it!

We can accomplish much with this simple idea. But first, a few words about the picture: To specify an $m\times n$ matrix $M$, one must specify all $mn$ entries $M_{ij}$. The index $i$ ranges from 1 to $m$—the dimension of the output space—and the index $j$ ranges from 1 to $n$—the dimension of the input space. Said differently, $i$ indexes the number of rows of $M$ and $j$ indexes the number of its columns. These indices can be included in the picture, if we like:

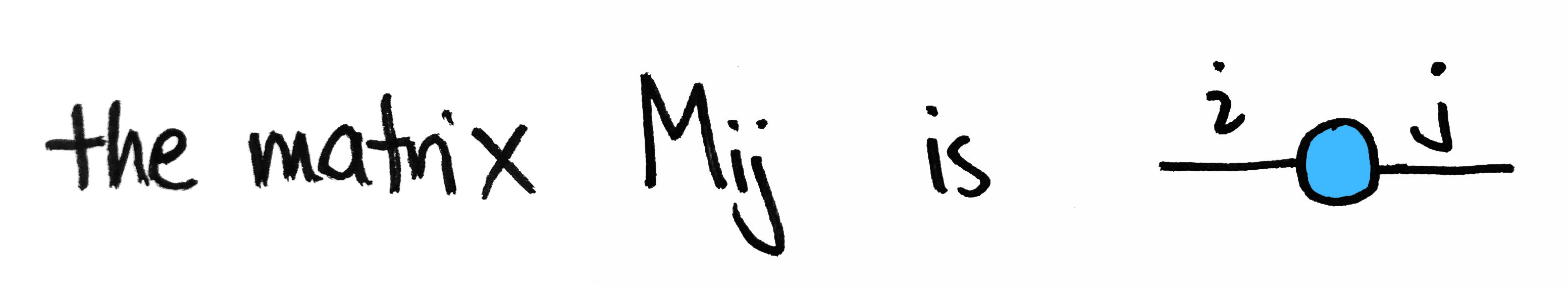
This idea generalizes very easily. A matrix is a two-dimensional array of numbers, while an $n$-dimensional array of numbers is called a tensor of order $n$ or an $n$-tensor. Like a matrix, an $n$-tensor can be  represented by a node with one edge for each dimension.

A number, for example, can be thought of as a zero-dimensional array, i.e. a point. It is thus a 0-tensor, which can be drawn as a node with zero edges. Likewise, a vector can be thought of as a one-dimensional array of numbers and hence a 1-tensor. It's represented by a node with one edge. A matrix is a two-dimensional array and hence 2-tensor. It's represented by a node with two edges. A 3-tensor is a three-dimensional array and hence a node with three edges, and so on.

Today I'd like to share an idea. It's a very simple idea. It's not fancy and it's certainly not new. In fact, I'm sure many of you have thought about it already. But if you haven't—and even if you have!—I hope you'll take a few minutes to enjoy it with me. Here's the idea:

‍

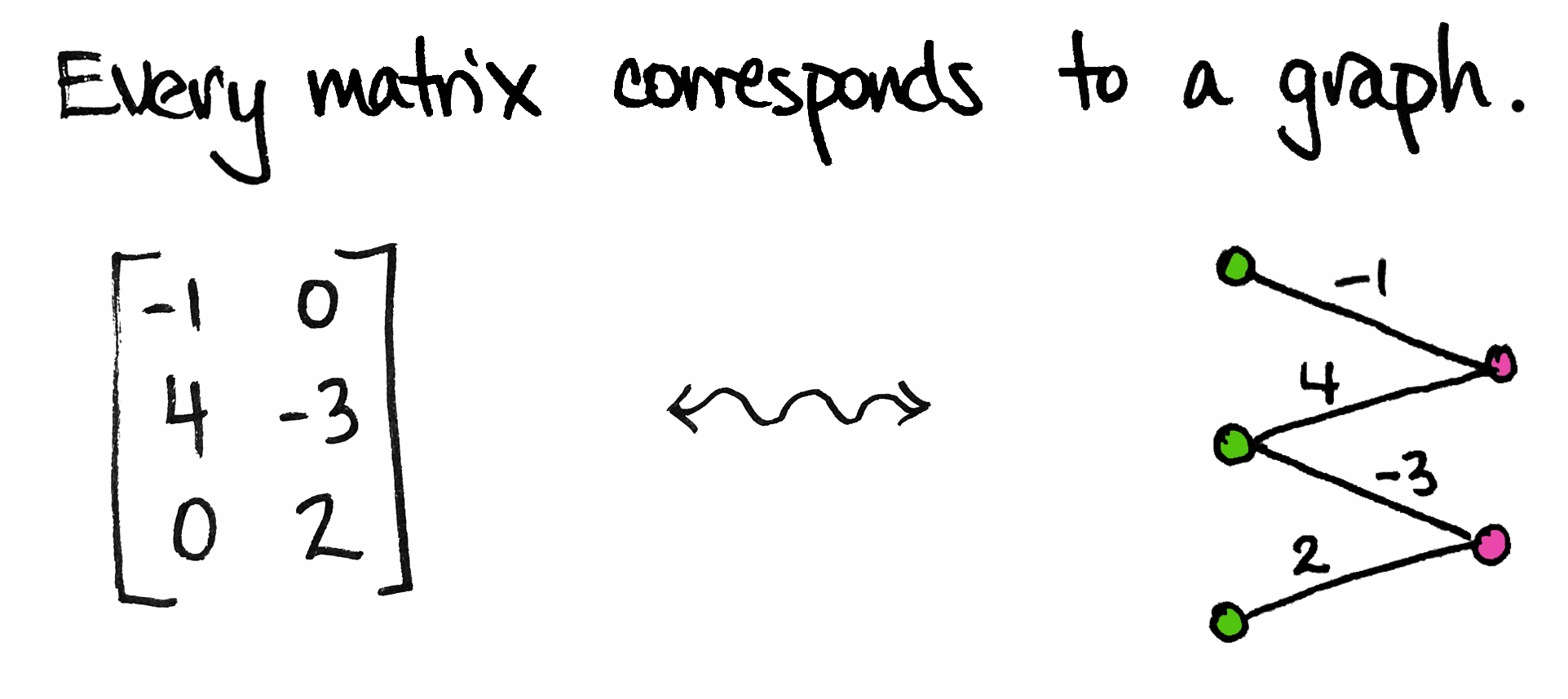
So simple! But we can get a lot of mileage out of it.

To start, I'll be a little more precise: every matrix corresponds to a weighted bipartite graph. By "graph" I mean a collection of vertices (dots) and edges; by "bipartite" I mean that the dots come in two different types/colors; by "weighted" I mean each edge is labeled with a number.

Once upon a time, we embarked on a mini-series about limits and colimits in category theory. Part 1 was a non-technical introduction that highlighted two ways mathematicians often make new mathematical objects from existing ones: by taking a subcollection of things, or by gluing things together. The first route leads to a construction called a limit, the second to a construction called a colimit.

The formal definitions of limits and colimits were given in Part 2. There we noted that one speaks of "the (co)limit of [something]." As we've seen previously, that "something" is a diagram—a functor from an indexing category to your category of interest. Moreover, the shape of that indexing category determines the name of the (co)limit: product, coproduct, pullback, pushout, etc.

In today's post, I'd like to solidify these ideas by sharing some examples of limits. Next time we'll look at examples of colimits. What's nice is that all of these examples are likely familiar to you—you've seen (co)limits many times before, perhaps without knowing it! The newness is in viewing them through a categorical lens. 

‍

‍

Recently I've been working on a dissertation proposal, which is sort of like a culmination of five years of graduate school (yay). The first draft was rough, but I sent it to my advisor anyway. A few days later I walked into his office, smiled, and said hello. He responded with a look of regret.

Advisor: I've been... remiss about your proposal.

[Remiss? Oh no. I can't remember what the word means, but it sounds really bad. The solemn tone must be a context clue. My heart sinks. I feel so embarrassed, so mortified. He's been remiss at me for days! Probably years! I think back to all the times I should've worked harder, all the exercises I never did. I knew This Day Would Come. I fight back the lump in my throat.]

Me: Oh no... oh no. I'm sorry. I shouldn't have sent it. It wasn't ready. Oh no....

Advisor: What?

Me: Hold on. What does remiss mean?

Advisor [confused, Googles remiss]: I think I just mean I haven't read your proposal.

Hi everyone. Here's a quick announcement: the Applied Category Theory 2019 school is now accepting applications! As you may know, I participated in ACT2018, had a great time, and later wrote a mini-book based on it. This year, it's happening again with new math and new people! As before, it consists of a five-month long, online school that culminates in a week long conference (July 15-19) and a week long research workshop (July 22-26, described below). Last year we met at the Lorentz Center in the Netherlands; this year it'll be at Oxford.

Daniel Cicala and Jules Hedges are organizing the ACT2019 school, and they've spelled out all the details in the official announcement, which I've copied-and-pasted it below. Read on for more! And please feel free to spread the word. Do it quickly, though. The deadline is soon!

APPLICATION DEADLINE: JANUARY 30, 2019

‍

Previously on the blog, we've discussed a recurring theme throughout mathematics: making new things from old things. Mathematicians do this all the time:

• When you have two integers, you can find their greatest common divisor or least common multiple.
• When you have some sets, you can form their Cartesian product or their union.
• When you have two groups, you can construct their direct sum or their free product.
• When you have a topological space, you can look for a subspace or a quotient space.
• When you have some vector spaces, you can ask for their direct sum or their intersection.
• The list goes on!

Today, I'd like to focus on a particular way to build a new vector space from old vector spaces: the tensor product. This construction often come across as scary and mysterious, but I hope to shine a little light and dispel a little fear. In particular, we won't talk about axioms, universal properties, or commuting diagrams. Instead, we'll take an elementary, concrete look:

Given two vectors $\mathbf{v}$ and $\mathbf{w}$, we can build a new vector, called the tensor product $\mathbf{v}\otimes \mathbf{w}$. But what is that vector, really? Likewise, given two vector spaces $V$ and $W$, we can build a new vector space, also called their tensor product $V\otimes W$. But what is that vector space, really?

Once upon a time, while in college, I decided to take my first intro-to-proofs class. I was so excited. "This is it!" I thought, "now I get to learn how to think like a mathematician."

You see, for the longest time, my mathematical upbringing was very... not mathematical. As a student in high school and well into college, I was very good at being a robot. Memorize this formula? No problem. Plug in these numbers? You got it. Think critically and deeply about the ideas being conveyed by the mathematics? Nope.

It wasn't because I didn't want to think deeply. I just wasn't aware there was anything to think about. I thought math was the art of symbol-manipulation and speedy arithmetic computations. I'm not good at either of those things, and I never understood why people did them anyway. But I was excellent at following directions. So when teachers would say "Do this computation," I would do it, and I would do it well. I just didn't know what I was doing.

By the time I signed up for that intro-to-proofs class, though, I was fully aware of the robot-symptoms and their harmful side effects.

Have you heard the buzz? Applied category theory is gaining ground! But, you ask, what is applied category theory? Upon first seeing those words, I suspect many folks might think either one of two thoughts:

1. Applied category theory? Isn't that an oxymoron?
2. Applied category theory? What's the hoopla? Hasn't category theory always been applied?

For those thinking thought #1, I'd like to convince you the answer is No way! It's true that category theory sometimes goes by the name of general abstract nonsense, which might incline you to think that category theory is too pie-in-the-sky to have any impact on the "real world." My hope is to convince you that that's far from the truth.

For those thinking thought #2, yes, it's true that ideas and results from category theory have found applications in computer science and quantum physics (not to mention pure mathematics itself), but these are not the only applications to which the word applied in applied category theory is being applied.

So what is applied category theory?

In this week's episode of PBS Infinite Series, I shared the following puzzle:

Consider a square in the xy-plane, and let A (an "assassin") and T (a "target") be two arbitrary-but-fixed points within the square. Suppose that the square behaves like a billiard table, so that any ray (a.k.a "shot") from the assassin will bounce off the sides of the square, with the angle of incidence equaling the angle of reflection. Puzzle: Is it possible to block any possible shot from A to T by placing a finite number of points in the square?

One day while doing a computation on the board in front of my students, I accidentally wrote 1 + 1 = 1. (No idea why.)

Student: Um, don't you mean 1 + 1 = 2?

Me (embarrassed): Oh right, thanks.

[Erases mistake. Pauses.] 

Wait. Is there a universe in which 1 + 1 = 1?

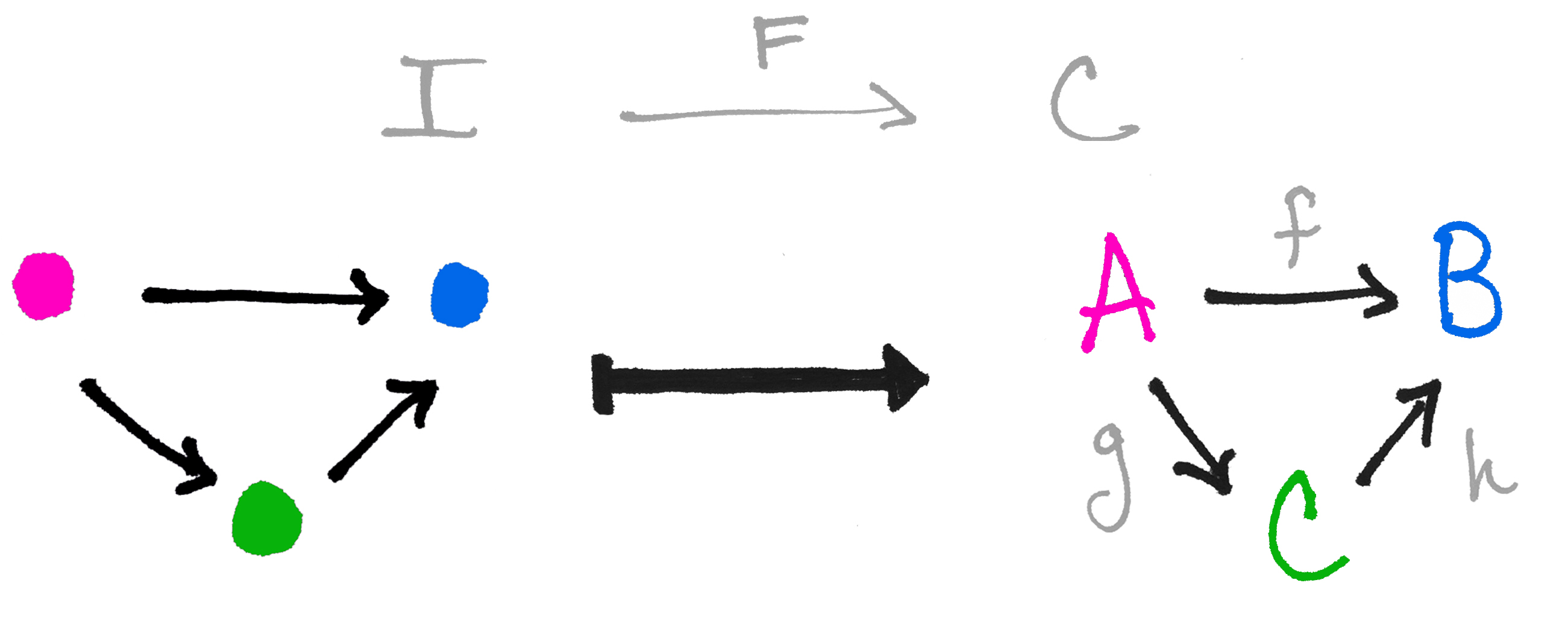
Welcome back to our mini-series on categorical limits and colimits! In Part 1 we gave an intuitive answer to the question, "What are limits and colimits?" As we saw then, there are two main ways that mathematicians construct new objects from a collection of given objects: 1) take a "sub-collection," contingent on some condition or 2) "glue" things together. The first construction is usually a limit, the second is usually a colimit. Of course, this might've left the reader wondering, "Okay... but what are we taking the (co)limit of ?" The answer? A diagram. And as we saw a couple of weeks ago, a diagram is really a functor.

Today I'd like to talk about Brouwer's Fixed Point Theorem. Literally! It's the subject of this week's episode on PBS Infinite Series. Brouwer's Fixed Point Theorem is a result from topology that says no matter how you stretch, twist, morph, or deform a disc (so long as you don't tear it), there's always one point that ends up in its original location.

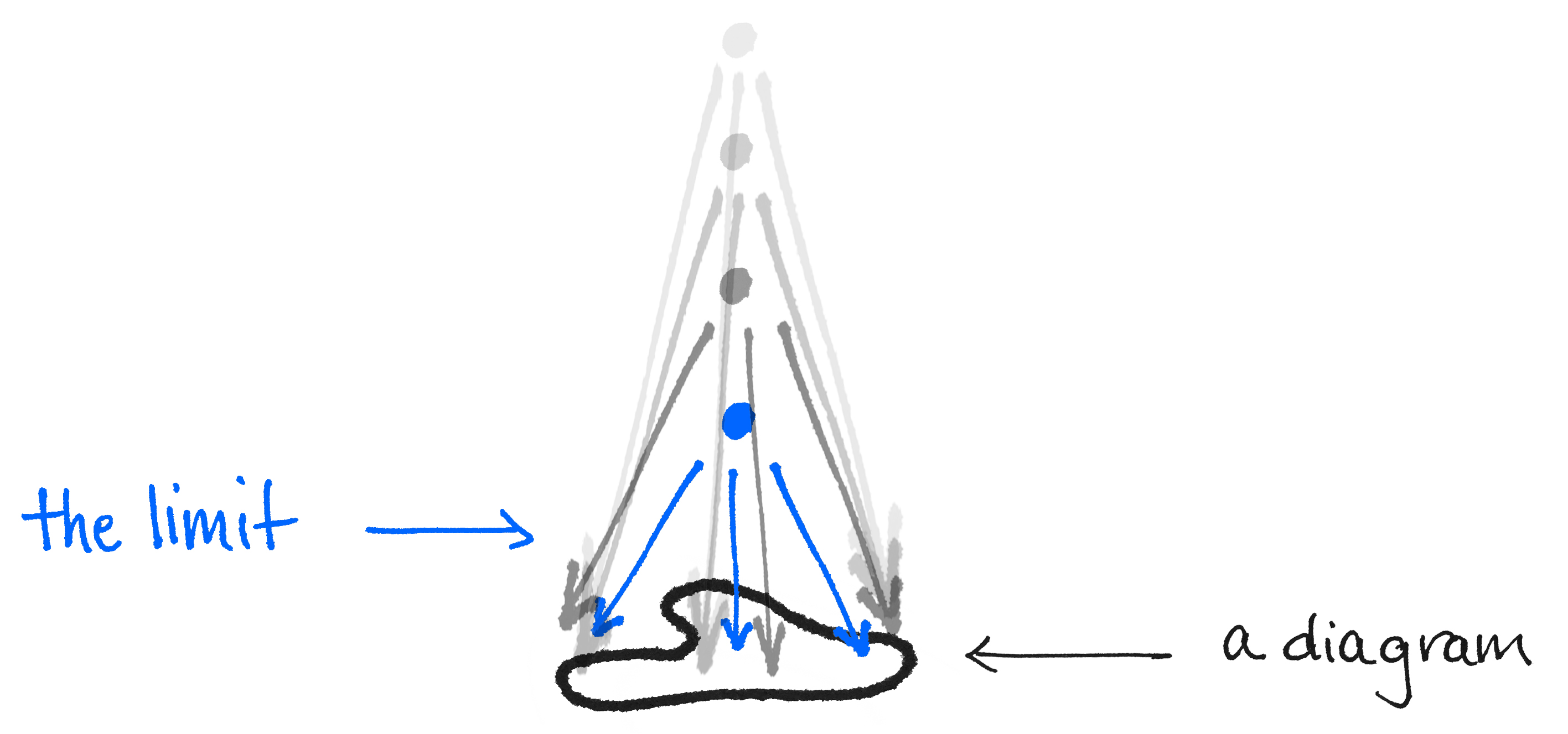
Last week was the start of a mini-series on limits and colimits in category theory. We began by answering a few basic questions, including, "What ARE (co)limits?" In short, they are a way to construct new mathematical objects from old ones. For more on this non-technical answer, be sure to check out Limits and Colimits, Part 1. Towards the end of that post, I mentioned that (co)limits aren't really related to limits of sequences in topology and analysis (but see here). There is however one similarity. In analysis, we ask for the limit of a sequence. In category theory, we also ask for the (co)limit OF something. But if that "something" is not a sequence, then what is it?

Answer: a diagram.

I'd like to embark on yet another mini-series here on the blog. The topic this time? Limits and colimits in category theory! But even if you're not familiar with category theory, I do hope you'll keep reading. Today's post is just an informal, non-technical introduction. And regardless of your categorical background, you've certainly come across many examples of limits and colimits, perhaps without knowing it! They appear everywhere--in topology, set theory, group theory, ring theory, linear algebra, differential geometry, number theory, algebraic geometry. The list goes on. But before diving in, I'd like to start off by answering a few basic questions.

This blog post is a continuation of today's episode on PBS Infinite Series, "Topology vs. 'a' Topology." My hope is that this episode and post will be helpful to anyone who's heard of topology and thought, "Hey! This sounds cool!" then picked up a book (or asked Google) to learn more, only to find those formidable three axioms of 'a topology' that, admittedly do not sound cool. But it turns out those axioms are what's "under the hood" of the whole topological business! So without further ado, let's pick up where we left off in the video.

In last last week's episode of PBS Infinite Series, we talked about different flavors of multiplication (like associativity and commutativity) to think about when multiplying things that aren't numbers. My examples of multiplying non-numbers were vectors and matrices, which come from the land of algebra. Today I'd like to highlight another example: We can multiply shapes!

Hi everyone! Here's a bit of exciting news: As of today, I'll be extending my mathematical voice from the blogosphere to the videosphere! In addition to Math3ma, you can now find me over at PBS Infinite Series, a YouTube channel dedicated to the wonderful world of mathematics.

Last week we introduced the definition of an operad: it's a sequence of sets or vector spaces or topological spaces or most anything you like (whose elements we think of as abstract operations), together with composition maps and a way to permute the inputs using symmetric groups. We also defined an algebra over an operad, which a way to realize each abstract operation as an actual operation. Now it's time for some examples!

If you browse through the research of your local algebraist, homotopy theorist, algebraic topologist or―well, anyone whose research involves an operation of some type, you might come across the word "operad." But what are operads? And what are they good for? Loosely speaking, operads―which come in a wide variety of types―keep track of various "flavors" of operations. 

☺️ I love math

😀 It's so cool.

Welcome to our third and final installment on the Yoneda lemma! In the past couple of weeks, we've slowly unraveled the mathematics behind the Yoneda perspective, i.e. the categorical maxim that an object  is completely determined by its relationships to other objects. Last week we divided this maxim into two points...

Last week we began a discussion about the Yoneda lemma. Though rather than stating the lemma (sans motivation), we took a leisurely stroll through an implication of its corollaries - the Yoneda perspective, as we called it:

 An object is completely determined by its relationships to other objects,

i.e.

by what the object "looks like" from the vantage point of each object in the category.

 But this left us wondering, What are the mathematics behind this idea? And what are the actual corollaries? In this post, we'll work to discover the answers.

In the words of Dan Piponi, it "is the hardest trivial thing in mathematics." The nLab catalogues it as "elementary but deep and central," while Emily Riehl nominates it as "arguably the most important result in category theory." Yet as Tom Leinster has pointed out, "many people find it quite bewildering."

And what are they referring to?

The Yoneda lemma.

"But," you ask, "what is the Yoneda lemma? And if it's just a lemma then - my gosh - what's the theorem?"

Dear Autocorrect,

No.

"Topos theory" is not the theory of tops. Or coats or shoes or hats or socks or gloves or slacks or scarves or shorts or skorts or--um, actually, what is topos theory?

“Zorn’s lemma” is not a result attributed to corn. Neither boiled corn, grilled corn, frozen corn, fresh corn, canned corn, popped corn, nor unicorns. Though I'm sure one of these is equivalent to the Axiom of Choice.

Mathematicians are a creative bunch, especially when it comes to naming things. And category theorists are no exception. So here's a little spin on this xkcd comic. It's inspired by a recent conversation I had on Twitter and, well, every category theory book ever.

Have you ever come across the words "commutative diagram" before? Perhaps you've read or heard someone utter a sentence that went something like, "For every [bla bla] there existsa [yadda yadda] such thatthe following diagram commutes." and perhaps it left you wondering what it all meant.

Not too long ago, my college-algebra students and I were chatting about graphing polynomials. At one point during our lesson, I quickly drew a smooth, wavy curve on the board and asked,

"How many roots would a polynomial with this graph have? Five? It crosses the x-axis five times."

A quick browse through my Instagram account and you might guess that I take notes. Lots of notes. And you'd be spot on! For this reason, I suppose, I am often asked the question, "How do you do it?!" Now while I don't think my note-taking strategy is particularly special, I am happy to share! I'll preface the information by stating what you probably already know: I LOVE to write.* I am a very visual learner and often need to go through the physical act of writing things down in order for information to "stick." So while some people think aloud (or quietly), 

I think on paper.

Once upon a time I wrote a six-part blog series on why the fundamental group of the circle is isomorphic to the integers. (You can read it here, though you may want to grab a cup of coffee first.) Last week, I shared a proof* of the same result. In one line. On Twitter. I also included a fewer-than-140-characters explanation. But the ideas are so cool that I'd like to elaborate a little more.

One of my students recently said to me, "I'm not good at math because I'm really slow." Right then and there, she had voiced what is one of many misconceptions that folks have about math.

But friends, speed has nothing to do with one's ability to do mathematics. In particular, being "slow" does not mean you do not have the ability to think about, understand, or enjoy the ideas of math.

Let me tell you....

Physicist Freeman Dyson once observed that there are two types of mathematicians: birds -- those who fly high, enjoy the big picture, and look for unifying concepts -- and frogs -- those who dwell on the ground, find beauty in the scenery close by, and enjoy the details.

Of course, both vantage points are essential to mathematical progress, and I often tend to think of myself as more of a bird.(I'm, uh, bird-brained?)

On Monday we concluded our mini-series on basic category theory with a discussion on natural transformations and functors. This led us to make the simple observation that the elements of any set are really just functions from the single-point set {✳︎} to that set. But what if we replace "set" by "group"? Can we view group elements categorically as well? The answer to that question is the topic for today's post, written by guest-author Arthur Parzygnat. 

Continuing our list of examples of natural transformations, here is Example #2 (double dual space of a vector space) and Example #3 (representability and Yoneda's lemma).

I hope you have enjoyed our little series on basic category theory. (I know I have!) This week we'll close out by chatting about natural transformations which are, in short, a nice way of moving from one functor to another. If you're new to this mini-series, be sure to check out the very first post, What is Category Theory Anyway? as well as What is a Category? and last week's What is a Functor?

I was at the grocery store earlier today, minding my own business, and while I was intently studying the lentil beans (Why are there so many options?) a man came down the aisle, pushing a cart with him. He then stopped in front of me, turned, looked me directly in the eyes and said,

Continuing yesterday's list of examples of functors, here is Example #3 (the chain rule from multivariable calculus), Example #4 (contravariant functors), and Example #5 (representable functors).

Next up in our mini series on basic category theory: functors! We began this series by asking What is category theory, anyway? and last week walked through the precise definition of a category along with some examples. As we saw in example #3 in that post, a functor can be viewed an arrow/morphism between two categories.

Hello friends! I've decided to launch a new series on the blog called crumbs! Every now and then, I'd like to share little stories -- crumbs, if you will -- from behind the scenes of Math3ma. To start us off, I posted (a slightly modified version of) the story below on January 23 on Facebook/Twitter/Instagram, so you may have seen this one already. Even so, I thought it'd be a good fit for the blog as well. I have a few more of these quick, soft-topic blurbs that I plan to share throughout the year. So stay tuned! I do hope you'll enjoy this newest addition to Math3ma.

As promised, here is the first in our triad of posts on basic category theory definitions: categories, functors, and natural transformations. If you're just now tuning in and are wondering what is category theory, anyway? be sure to follow the link to find out!

A category $\mathsf{C}$ consists of some data that satisfy certain properties...

A quick browse through my Twitter or Instagram accounts, and you might guess that I've had category theory on my mind. You'd be right, too! So I have a few category-theory themed posts lined up for this semester, and to start off, I'd like to (attempt to) answer the question, What is category theory, anyway? for anyone who may not be familiar with the subject.

Now rather than give you a list of definitions--which are easy enough to find and may feel a bit unmotivated at first--I thought it would be nice to tell you what category theory is in the grand scheme of (mathematical) things. You see, it's very different than other branches of math....

If you've been following this blog for a while, you'll know that I have strong opinions about the misconception that "math is only for the gifted." I've written about the importance of endurance and hard work several times. Naturally, these convictions carried over into my own classroom this past semester as I taught a group of college algebra students.

Whether they raised their hand during a lecture and gave a "wrong" answer, received a less-than-perfect score on an exam or quiz, or felt completely confused during a lesson, I tried to emphasize that things aren't always as bad as they seem...

Over the past few weeks, we've been chatting about quotient groups  in hopes of answering the question, "What's a quotient group, really?" In short, we noted that the quotient of a group $G$ by a normal subgroup $N$ is a means of organizing the group elements according to how they fail---or don't fail---to satisfy the property required to belong to $N$. The key point was that there's only one way to belong to $N$, but generally there may be several ways to fail to belong. 

Last week we took an intuitive peek into the First Isomorphism Theorem as one example in our ongoing discussion on quotient groups. Today we'll explore another quotient that you've likely come across, namely that of a group by its center.

Welcome back to our little discussion on quotient groups! (If you're just now tuning in, be sure to check out "What's a Quotient Group, Really?" Part 1 and Part 2!) We're wrapping up this mini series by looking at a few examples. I'd like to take my time emphasizing intuition, so I've decided to give each example its own post. Today we'll take an intuitive look at the quotient given in the First Isomorphism Theorem.

Today we're resuming our informal chat on quotient groups.  Previously we said that belonging to a (normal, say) subgroup $N$ of a group $G$ just means you satisfy some property. For example, $5\mathbb{Z}\subset\mathbb{Z}$ means "You belong to $5\mathbb{Z}$ if and only if you're divisible by 5". And the process of "taking the quotient" is the simple observation that every element in $G$ either

#1) belongs to N            or            #2) doesn't belong to N

and noting that...

I realize that most of my posts for the past, er, few months have been about some pretty hefty duty topics. Today, I'd like to dial it back a bit and chat about some basic group theory! So let me ask you a question: When you hear the words "quotient group," what do you think of? In case you'd like a little refresher, here's the definition...

Last time we chatted about a pervasive theme in mathematics, namely that objects are determined by their relationships with other objects, or more informally, you can learn a lot about an object by studying its interactions with other things. Today I'd to give an explicit illustration of this theme in the case when "objects" = topological spaces and "relationships with other objects" = continuous functions. The goal of this post, then, is to convince you that the topology on a space  is completely determined by the set of all continuous functions to it.

Yes, I agree. The title for this post is a little pretentious. It's certainly possible that there are other mathematical secrets that are more obvious than this one, but hey, I got your attention, right? Good. Because I'd like to tell you about an overarching theme in mathematics - a mathematical mantra, if you will. A technique that mathematicians use all the time to, well, do math. 

It's possible that a set $X$ can be endowed with two or more topologies that are comparable. Over the years, mathematicians have used various  words to describe the comparison: a topology $\tau_1$ is said to be coarser than another topology $\tau_2$, and we write $\tau_1\subseteq\tau_2$, if every open set in $\tau_1$ is also an open set in $\tau_2$. In this scenario, we also say $\tau_2$ is finer than $\tau_1$. But other folks like to replace "coarser" by "smaller" and "finer" by "larger." Still others prefer to use "weaker" and "stronger." But how can we keep track of all of this? 

In recent months, several of you have asked me to recommend resources for various subjects in mathematics. Well, folks, here it is! I've finally rounded up a collection of books, PDFs, videos, and websites that I found helpful while studying for my intro-level graduate courses. 

Today I'm talking about about qualifying exams! But no, I won't be dishing out advice on preparing for these exams. Tons of excellent advice is readily available online, so I'm not sure I can contribute much that isn't already out there. However, it's that very web-search that has prompted me to write this post.

You see, before I started graduate school I had heard of these rites-of-passage called the qualifying exams.* And to be frank, I thought they sounded terrifying.

This is the last in a four-part series in which we prove that the automorphisms of the unit disc, upper half plane, complex plane, and Riemann sphere each take on a different form. Today our focus is on the Riemann sphere.

This is part three of a four-part series in which we prove that the automorphisms of the unit disc, upper half plane, complex plane, and Riemann sphere each take on a different form. Today our focus is on the complex plane.

This is part two of a four-part series in which we prove that the automorphisms of the unit disc, upper half plane, complex plane, and Riemann sphere each take on a different form. Today our focus is on the upper half plane.

This is part one of a four-part series in which we prove that the automorphisms of the unit disc, upper half plane, complex plane, and Riemann sphere each take on a different form. Today our focus is on the unit disc.

In this post we ramble on about Riemann surfaces, the uniformization theorem, universal covers, and two secret (or not-so-secret!) techniques that mathematicians use to study a given space. Our intent is to provide motivation for an upcoming mini-series on the automorphisms of the unit disc, upper half plane, complex plane, and Riemann sphere.

Here's another unspoken rule of mathematics: English doesn't always commute!

Word order is important...

Next up on Good Reads: The Princeton Companion to Mathematics, edited by Fields medalist Timothy Gowers. This book is an exceptional resource! With over 1,000 pages of mathematics explained by the experts for the layperson, it's like an encyclopedia for math, but so much more. Have you heard about category theory but aren't sure what it is? There's a chapter for that! Seen the recent headlines about the abc conjecture but don't know what it's about? There's a chapter for that! Need a crash course in general relativity and Einstein's equations, or the P vs. NP conjecture, or C*-algebras, or the Riemann zeta function, or Calabi-Yau manifolds? There are chapters for all of those and more.

You know the routine. You come across a topological space $X$ and you need to find its fundamental group. Unfortunately, $X$ is an unfamiliar space and it's too difficult to look at explicit loops and relations. So what do you do? You look for another space $Y$ that is homotopy equivalent to $X$ and whose fundamental group $\pi_1(Y)$ is much easier to compute. And voila! Since $X$ and $Y$ are homotopy equivalent, you know $\pi_1(X)$ is isomorphic to $\pi_1(Y)$. Mission accomplished.

 Below is a list of some homotopy equivalences which I think are pretty clever and useful to keep in your back pocket for, say, a qualifying exam or some other pressing topological occasion.

A while ago I wrote a post in response to a great Slate article reminding us that math - like writing - isn't something that anyone is good at without (at least a little!) effort. As the article's author put it, "no one is born knowing the axiom of completeness." Since then, I've come across a few other snippets of mathematical candor that I found both helpful and encouraging. And since final/qualifying exam season is right around the corner, I've decided to share them here on the blog for a little morale-boosting.

I was recently (avoiding doing my homology homework by) reading through some old poems by Shel Silverstein, author of The Giving Tree, A Light in the Attic, and Falling Up to name a few. Feeling inspired, I continued to procrastinate by writing a little poem of my own - about homology, naturally!

My goal for today is to provide a step-by-step guideline for classifying closed surfaces. (By 'closed,' I mean a surface that is compact and has no boundary.) The information below may come in handy for any topology student who needs to know just the basics (for an exam, say, or even for other less practical (but still mathematically elegant) endeavors) so there won't be any proofs today. Given a polygon with certain edges identified, we can determine the surface that it represents in just three easy steps:

Yesterday I received a disheartening 44/50 on a homework assignment. Okay okay, I know. 88% isn't bad, but I had turned in my solutions with so much confidence that admittedly, my heart dropped a little (okay, a lot!) when I received the grade. But I quickly had to remind myself, Hey! Grades don't matter.

Have you been on the hunt for a good introductory-level real analysis book? Look no further! The underrated Real Analysis by N. L. Carothers is, in my opinion, one of the best out there. Real analysis has a reputation for being a fearful subject for many students, but this text by Carothers does a great job of mitigating those fears. Aimed towards advanced undergraduate and early graduate students, it is written in a fantastically warm and approachable manner without sacrificing too much rigor. The text is intentionally conversational (which I love!) and includes plenty of exercises and illustrations, all the while informing the reader of context and historical background along the way. 

A while ago, I wrote about the importance of open sets in topology and how the properties of a topological space $X$ are highly dependent on these special sets. In that post, we discovered that the real line $\mathbb{R}$ can either be compact or non-compact, depending on which topological glasses we choose to view $\mathbb{R}$ with. Today, I’d like to show you another such example - one which has a surprising consequence!

Last time we proved that the pseudo-hyperbolic metric on the unit disc in ℂ is indeed a metric. In today’s post, we use this fact to verify Lindelöf’s inequality which says, "Hey! Want to apply Schwarz's Lemma but don't know if your function fixes the origin? Here's what you do know...."

In this post, we define the pseudo-hyperbolic metric on the unit disc in ℂ and prove it does indeed satisfy the conditions of a metric.

Love and Math by Edward Frenkel is an excellent book about the hidden beauty and elegance of mathematics. It is primarily about Frenkel’s work on the Langlands Program (a sort of grand unified theory of mathematics) and its recent connections to quantum physics. Yet the author's goal is not merely to inform but rather to convert the reader into a lover of math. While Frenkel acknowledges that many view mathematics as an “insufferable torment… pure torture, or a nightmare that turns them off,” he also feels that math is “too precious to be given away to the ‘initiated few.’” In the preface he writes...

The goal of today's post is to prove that the fundamental group of the real projective plane, is isomorphic to $\mathbb{Z}/2\mathbb{Z}$ And unlike our proof for the fundamental group of the circle, today's proof is fairly short, thanks to the van Kampen theorem! To make our application of the theorem a little easier, we start with a simple observation: projective plane - disk = Möbius strip. Below is an excellent animation which captures this quite clearly....

There are two definitions of absolute continuity out there. One refers to an absolutely continuous function and the other to an absolutely continuous measure. And although the definitions appear unrelated, they are in fact very much related, linked together by Lebesgue's Fundamental Theorem of Calculus. This is the second of a two-part series where we explore that relationship.

There are two definitions of absolute continuity out there. One refers to an absolutely continuous function and the other to an absolutely continuous measure. And although the definitions appear unrelated, they are in fact very much related, linked together by Lebesgue's Fundamental Theorem of Calculus. This is part one of a two-part series where we explore that relationship.

In sum, the sufficient condition (a.k.a. the "if" direction) allows you to get what you want. That is, if you assume the sufficient condition, you'll obtain your desired conclusion. It's enough. It's sufficient. 

On the other hand, the necessary condition (a.k.a. the "only if" direction) is the one you must assume in order to get what you want. In other words, if you don't have the necessary condition then you can't reach your desired conclusion. It is necessary. 

Welcome to the final post in a six-part series where we prove that the fundamental group of the circle $\pi_1(S^1)$ is isomorphic to $\mathbb{Z}$. Today we prove two lemmas (the path- and homotopy-lifting properties) that were used in parts four and five. The proof follows that found in Hatcher's Algebraic Topology section 1.1.

Below is a general method —a recipe, if you will —for computing the universal cover of the wedge sum $X\vee Y$ of arbitrary topological spaces $X$ and $Y$. This is simply a short-and-quick guideline that my prof mentioned in class, and I thought it'd be helpful to share on the blog. To help illustrate each step, we'll consider the case when $X=T^2$ is the torus and $Y=S^1$ is the circle.