What is Category Theory Anyway?

A quick browse through my Twitter or Instagram accounts, and you might guess that I've had category theory on my mind. You'd be right, too! So I have a few category-theory themed posts lined up for this semester, and to start off, I'd like to (attempt to) answer the question, What is category theory, anyway? for anyone who may not be familiar with the subject.
Now rather than give you a list of definitions--which are easy enough to find and may feel a bit unmotivated at first--I thought it would be nice to tell you what category theory is in the grand scheme of (mathematical) things. You see, it's very different than other branches of math. Rather than being another sibling lined up in the family photograph, it's more like a common gene that unites them in the first place.
Let me explain.
The grand scheme of (mathematical) things
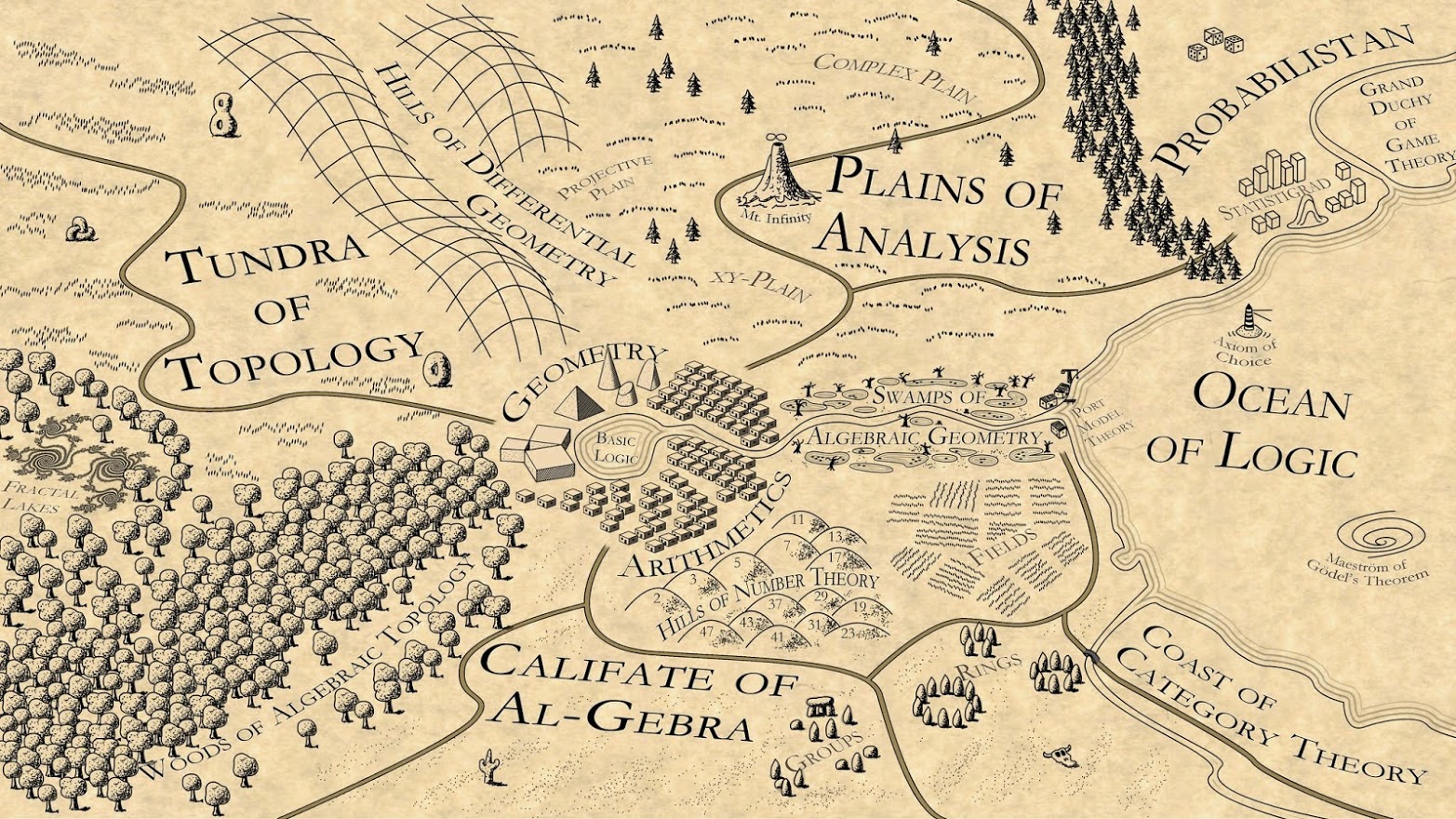
Martin Kuppe once created a wonderful map of the mathematical landscape, which he dubbed "Mathematistan." You'll notice that the "coast of category theory" is located in the lower right corner. In my opinion, category theory isn't so much another country-on-the-map as it is a means of getting a bird's-eye-view of the entire landscape. It's what lifts our feet off the grass and provides us with a sweeping vista from the sky.
With this vantage point, it becomes evident that different areas of math share common patterns/trends/structures. This becomes extraordinarily useful when you want to solve a problem in one realm (say, topology) but don't have the right tools at your disposal. By transporting the problem to a different realm (say, algebra), you can see the problem in a different light and perhaps discover new tools, and the solution may become much easier.
The bridges between realms are also provided by category theory. It explicitly identifies the realms' common structures: each has objects in it (set theory has sets, group theory has groups, topology has topological spaces,...) that can relate to each other (sets relate via functions, groups relate via homomorphisms, topological spaces relate via continuous functions,...) in sensible ways (composition and associativity).
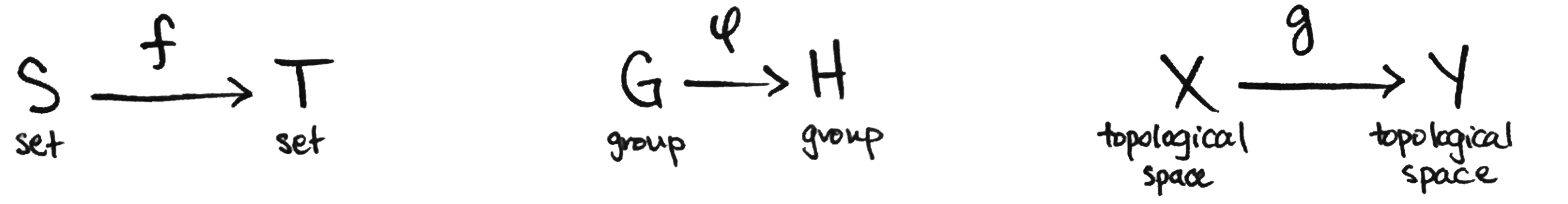
A category, then, is any collection of objects that can relate to each other via morphisms in sensible ways, like composition and associativity. As Barry Mazur once remarked, this is a "template" for all of mathematics: depending on what you feed into the template, you'll recover one of the mathematical realms. So the collection of sets with functions forms a category, as does the collection of groups with group homomorphisms, and topological spaces with continuous functions. In addition to these, here are some other categories you're probably familiar with:
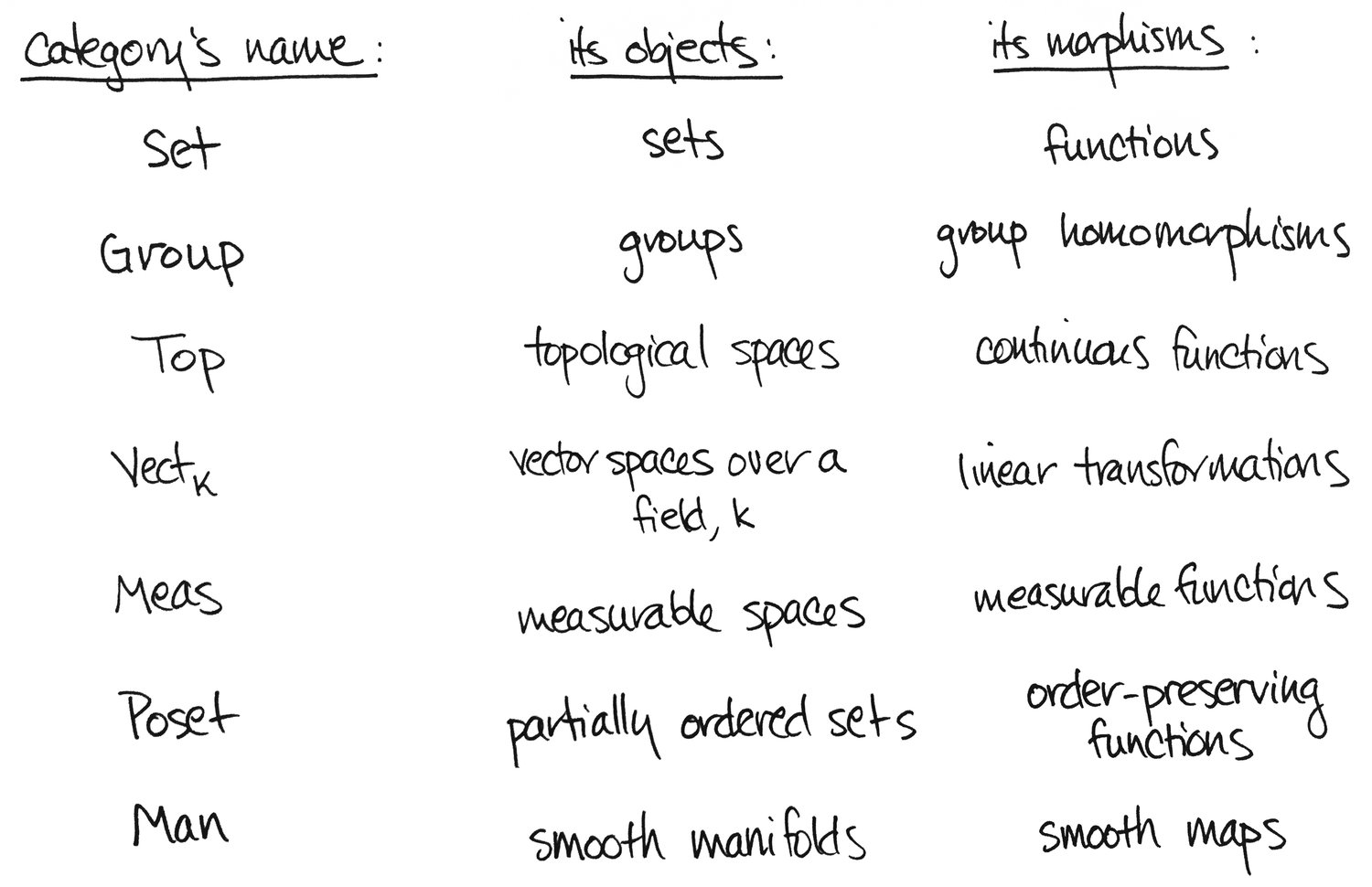
It's all about relationships!
One of the features of category theory is that it strips away a lot of detail: it's not really concerned with the elements in your set, or whether your group is solvable or not, or if your topological space has a countable basis. So you might wonder---and rightly so---How can it possibly be useful?
Mathematical objects are determined by--and understood by--the network of relationships they enjoy with all the other objects of their species.
- Barry Mazur
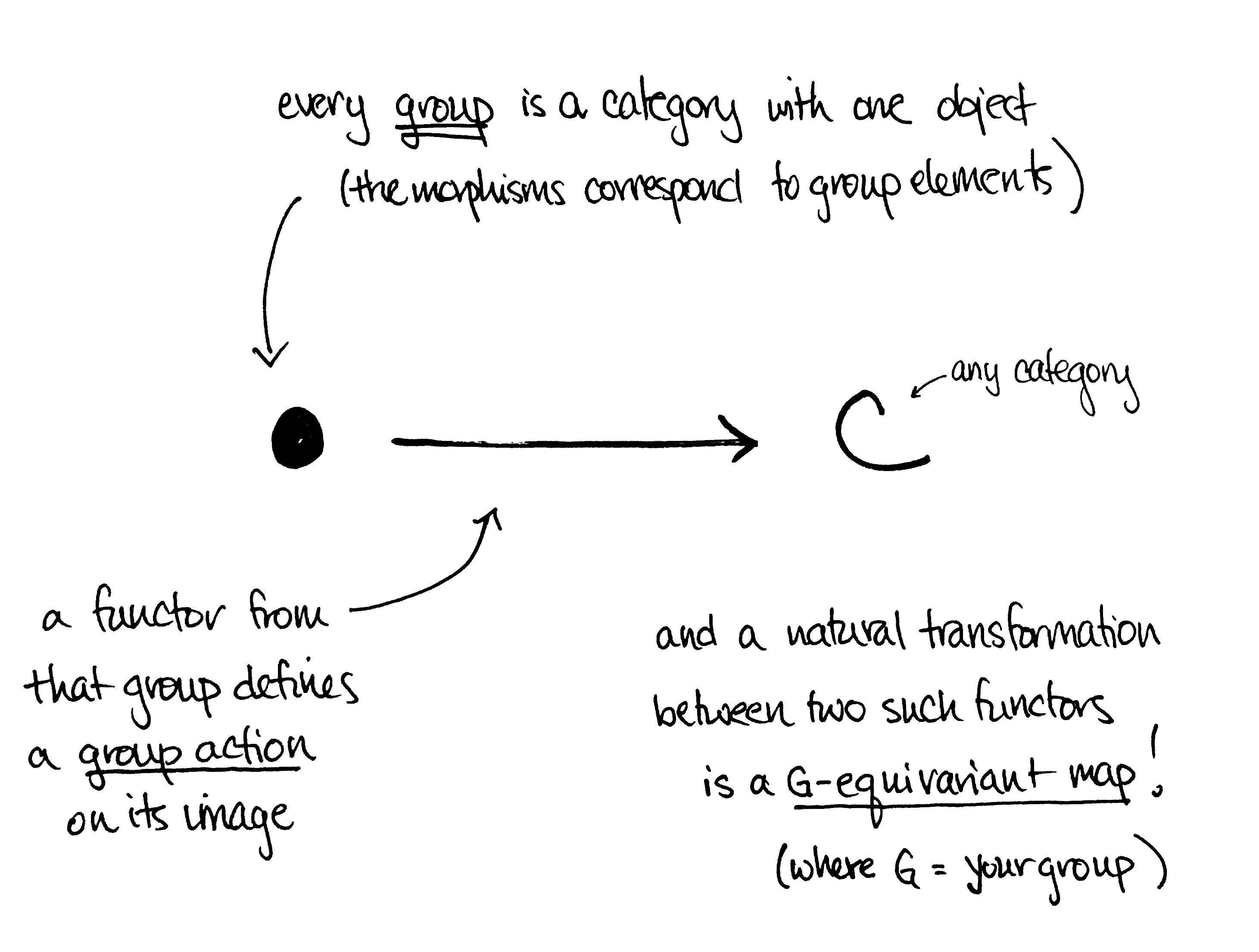
Well, the advantage of ignoring details is that your attention is diverted from the actual objects to the relationships betweenthem (that is, on the morphisms). Naturally, then, you're prompted to also ask about relationships between categories. These are called functors. But why stop there? What about the relationships between those relationships? These are called natural transformations. (And yes, you can ask a hierarchy of questions: "What about the relationships between the relationships between the relationships between the...?" This leads to infinity categories. [And a possible brain freeze.] For more, see here.) As pie-in-the-sky as this may sound, these ideas---categories, functors, and natural transformations---lead to a treasure trove of theory that shows up almost everywhere.
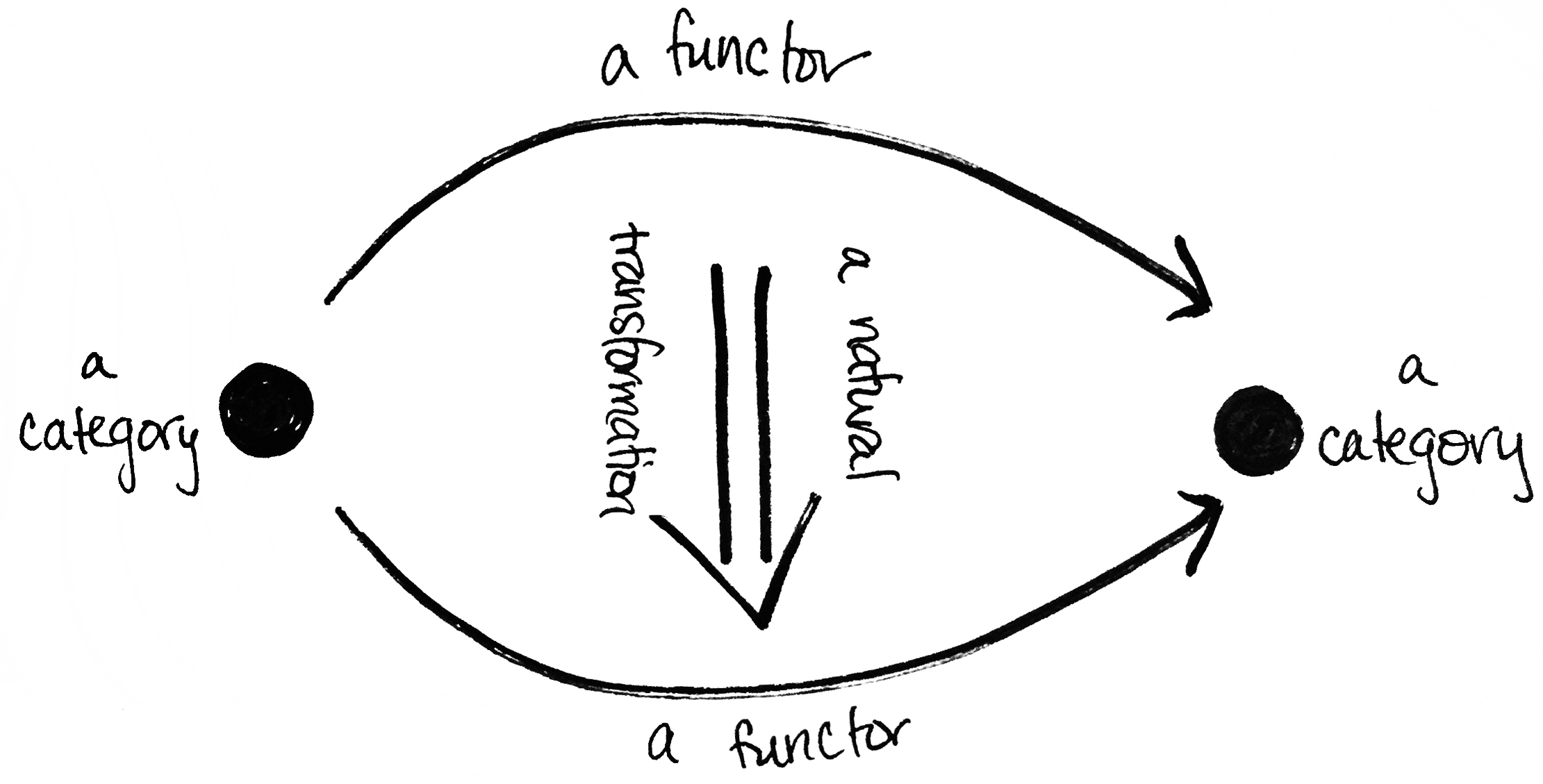
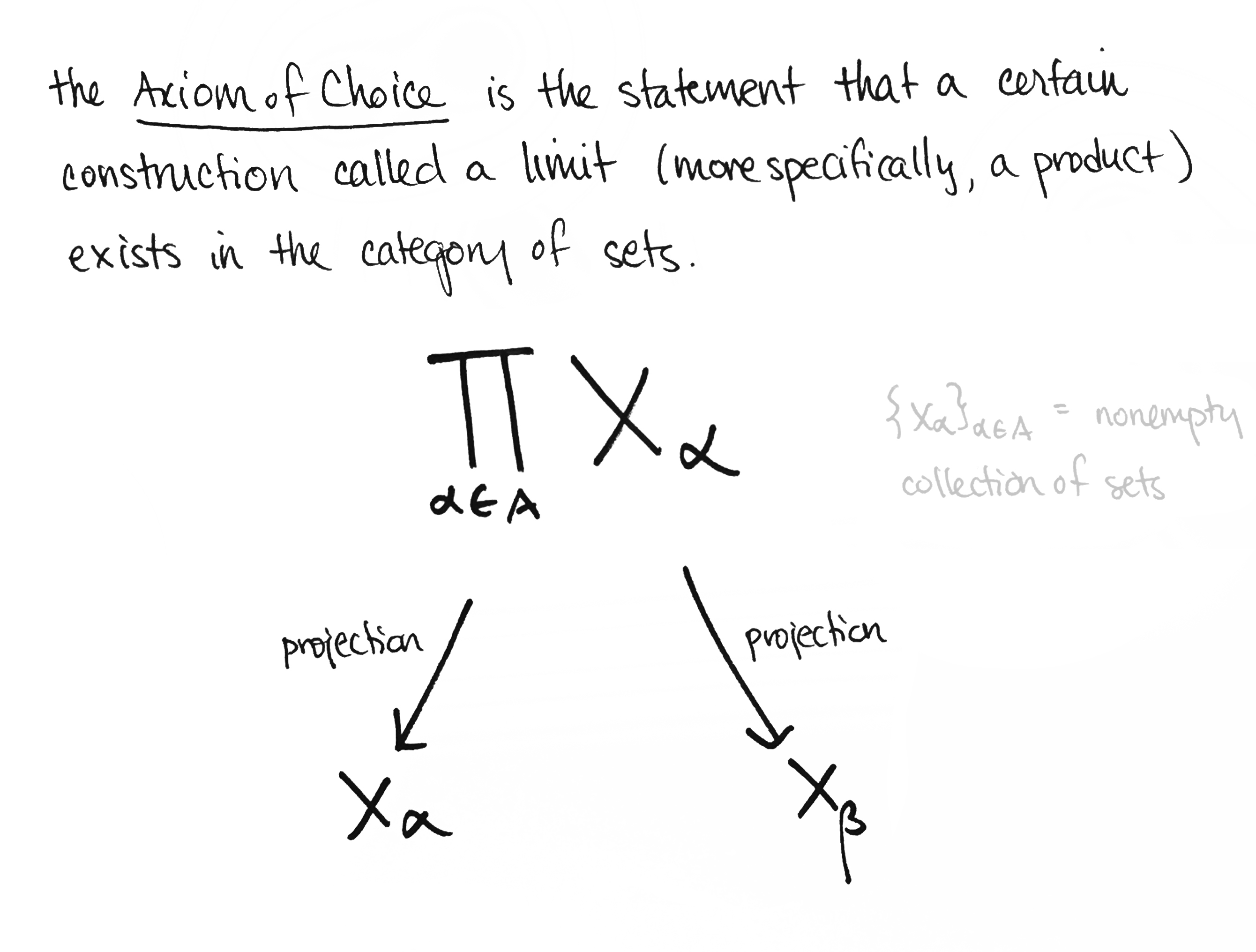
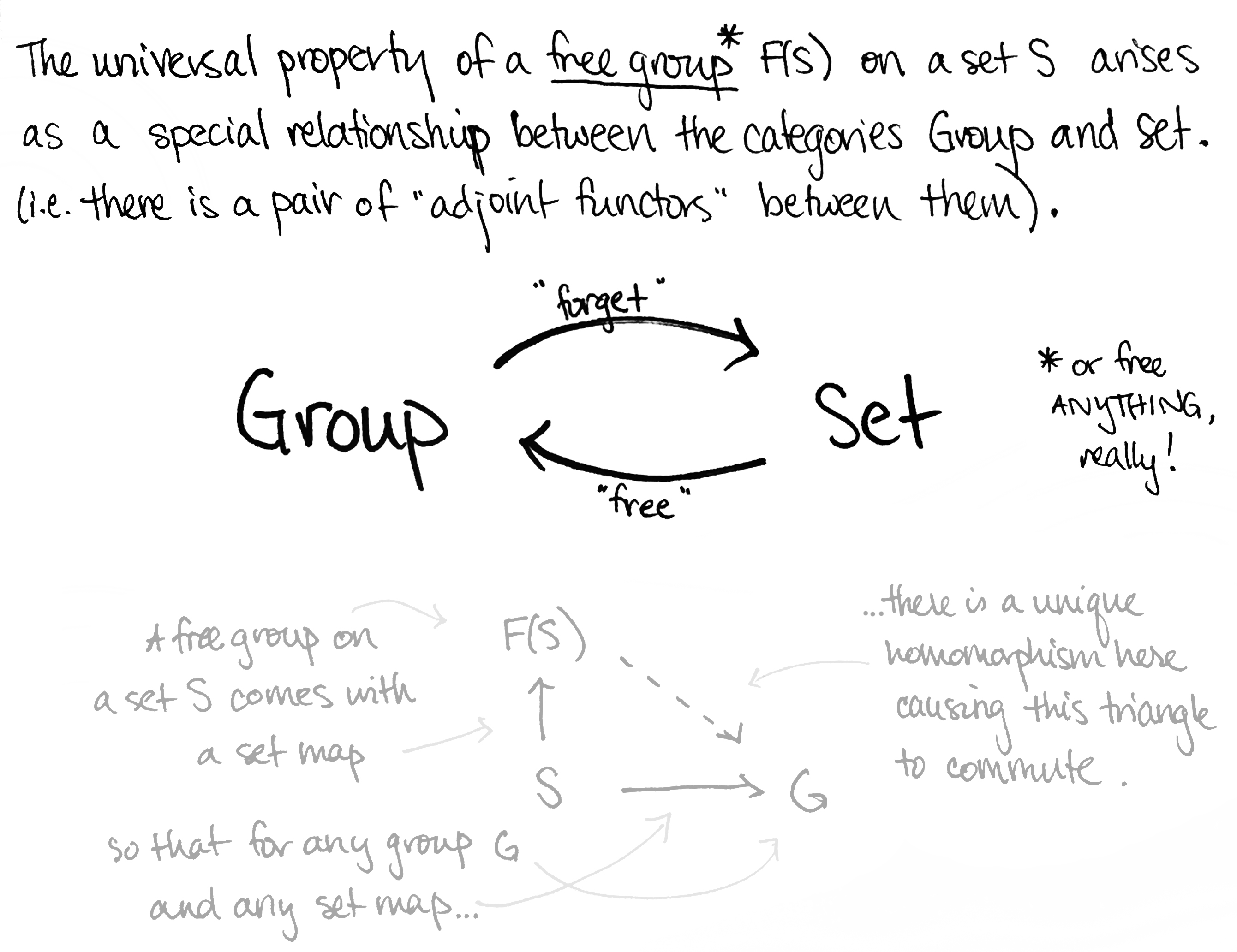
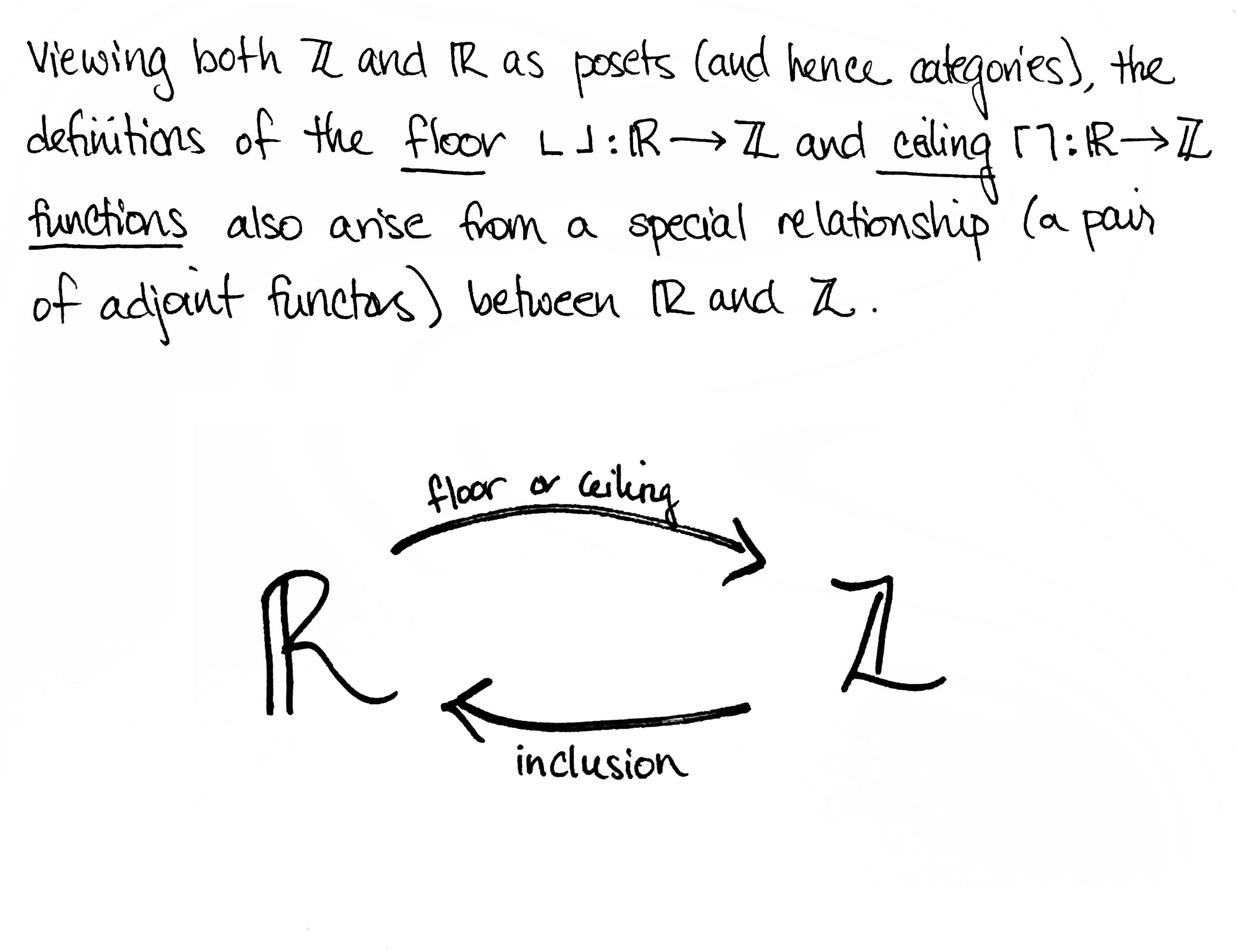
Below is some evidence, most of which I've taken from Emily Riehl's excellent book Category Theory in Context.










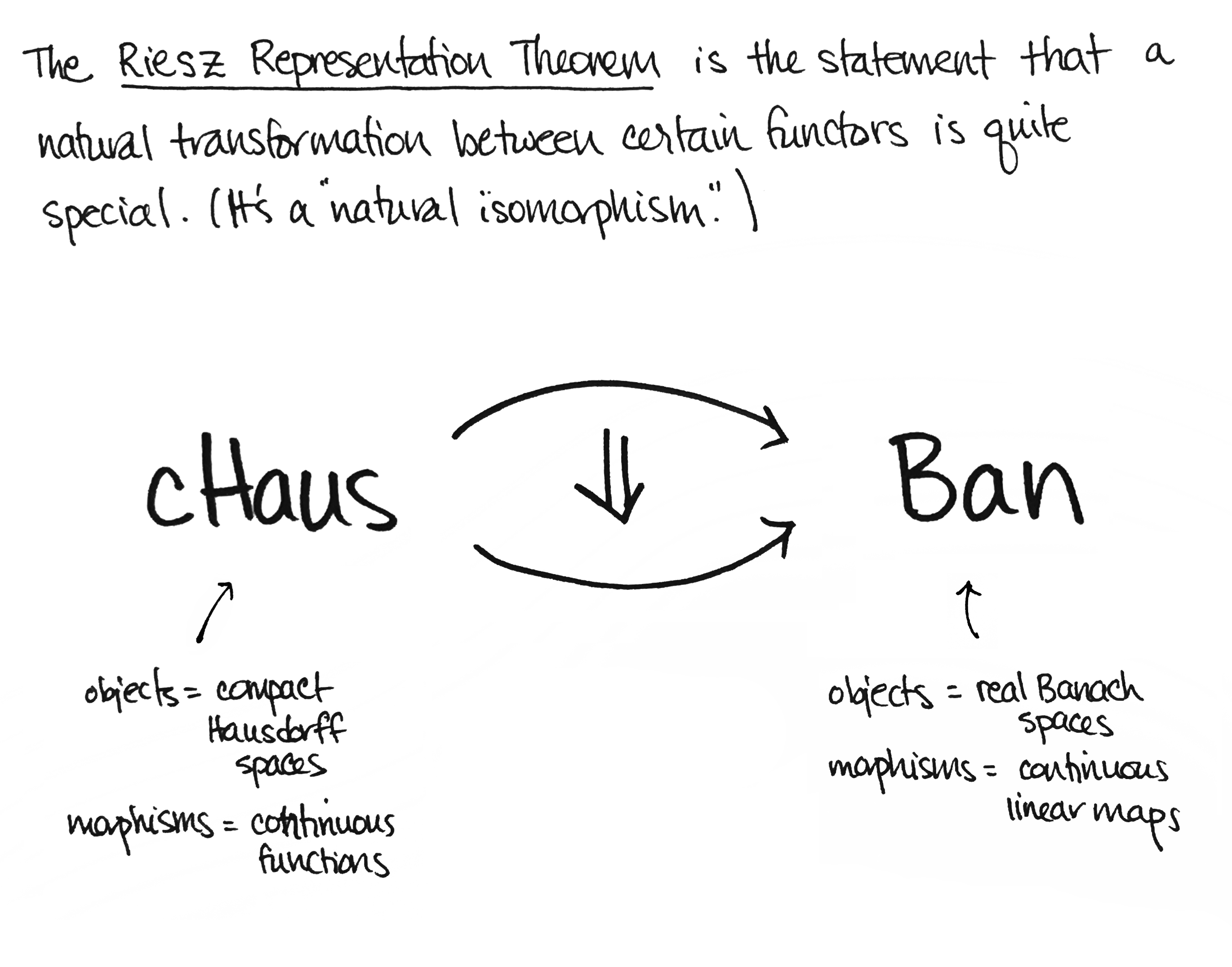

But why category theory?
I realize that categories can be a bit like anchovies: some folks love 'em, some folks don't, and for some folks they're an acquired taste. It's true that category theory may not help you find a delta for your epsilon, or determine if your group of order 520 is simple, or construct a solution to your PDE. For those endeavors, we do have to put our feet back on the ground. But thinking categorically can help serve as a beacon---it can strengthen your intuition, sharpen your insight---as you trek through the nooks and crannies of your favorite mathematical realms. (As Freeman Dyson would say, we need both birds and frogs to foster mathematical progress!)
I also think the attractiveness of category theory depends heavily on your goal as a mathematician. It greatly appeals to me because I love learning about connections between seemingly unrelated things. This is actually what got me into math in the first place---not a particular problem/phenomena in geometry or analysis or algebra, but the mere idea that there are underlying/hidden connections among them just to be uncovered.
All in all, the pervasiveness of category theory throughout mathematics has become quite apparent. So whatever your mathematical goals may be, I think learning a bit about categories will be well worth your time! Here are a few good places to start:
- If you'd like more motivation, I highly recommend Barry Mazur's wonderful article When is one thing equal to some other thing? And for a friendly, gentle introduction to categories, you may enjoy Conceptual Mathematics: A First Introduction to Categories by William Lawvere and Stephen Schanuel.
- Basic Category Theory by Tom Leinster should be accessible at the undergraduate level ("This is not a sophisticated text." is the first sentence.) and is certainly accessible at the graduate level. I also like the book by Emily Riehl that I referred to earlier. A free PDF is available on her website.
- For a more applied point of view, take a look at Category Theory for the Sciences by David Spivak. You will also find some exciting applications of category theory in Physics, Topology, Logic, and Computation: A Rosetta Stone by John Baez and Mike Stay.
- The classic is Categories for the Working Mathematician by Saunders Mac Lane who, along with Samuel Eilenberg, developed category theory in the 1940s.
- Here is an article by John D. Cook in which he talks about the (usual, Cartesian) product from a categorical perspective--notice the emphasis on relationships!
- Once you've learned the basic definitions, here are a few YouTube videos (including some by Eugenia Cheng) on more advanced categorial topics.
- And, as a catch-all, here's a link that contains a slew of online books, articles, lecture notes, and videos!
During the next few weeks, I'll go through the precise definitions of a category, a functor, and a natural transformation along with some examples. You can, of course, find them in any of the resources above, but it'll be nice to have them on the blog, too. Until then!



Good general theory does not search for the maximum generality, but for the right generality.
- Saunders Mac Lane
