The Fundamental Group of the Circle, Part 1

Welcome to part one of a six-part series where we prove that the fundamental group of the circle $\pi_1(S^1)$ is isomorphic to $\mathbb{Z}$. This proof follows that from Hatcher's Algebraic Topology section 1.1, and so I will assume the reader knows the definition of a homotopy, a loop, fundamental groups, etc. When I read this proof for the first time, I was - to put it bluntly - lost. Don't get me wrong though - the ideas aren't difficult at all, but filtering through the notation/language was a little daunting. So I decided to rewrite everything (with lots of pictures!) to fill in some of the "white space between the lines" of Hatcher's proof. Also, the ideas found here appear over and over again in a study on covering spaces (Hatcher's section 1.3), so taking our time through this material will be worthwhile. But brevity and accessibility seem to be inversely proportional in mathematics, so this series is somewhat lengthy. Fair warning!
Let me begin by stating the theorem, then I'll give the outline of the proof.
Theorem: The map $\Phi:\mathbb{Z}\to \pi_1(S^1)$ given by $n\mapsto [\omega_n]$, where $\omega_n(s)=(\cos{2\pi ns},\sin{2\pi ns})$ for $s\in[0,1]$ is a loop in $S^1$ based at $(1,0)$, is an isomorphism. In other words $\pi_1(S^1)\cong \mathbb{Z}$.
Outline of the proof:
Part 1: Set-up/observations
Part 2: Show $\Phi$ is well defined
Part 3: Show $\Phi$ is a group homomorphism
Part 4: Show $\Phi$ is surjective
Part 5: Show $\Phi$ is injective (Note: parts 4 and 5 require two lemmas whose proofs we will defer until part 6)
Part 6: Prove the two lemmas used in parts 4 and 5
Let's get started!
Set-up/Observations
As Hatcher summarizes, the idea is to compare paths in $S^1$ with paths in $\mathbb{R}$ via the projection map $p:\mathbb{R}\to S^1$ which sends $s\mapsto (\cos{2\pi s},\sin{2\pi s})$. Embedding $\mathbb{R}$ into $\mathbb{R}^3$ as a helix, we can visualize the projection map this way:
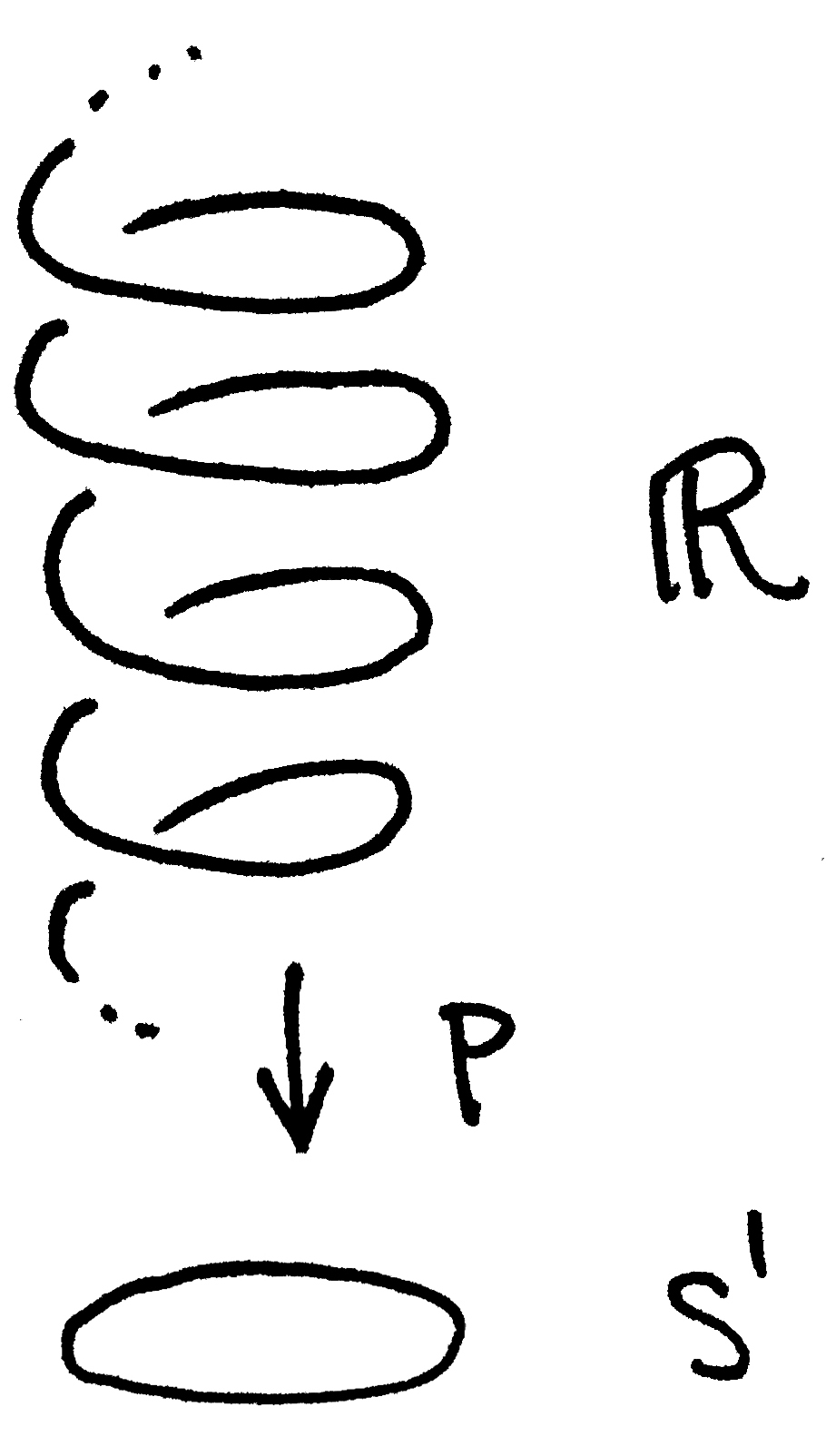
But let's be a little more specific. Let $I=[0,1]$ denote the unit interval in $\mathbb{R}$ and for $n\in \mathbb{Z}$, define $\widetilde{\omega}_n:I\to \mathbb{R}$ by $\widetilde{\omega}_n(s)=ns.$ Notice this is a path which is simply a straight line from $0$ to $n$. In the helix, $\widetilde{\omega}_n(I)$ starts at $0$ and winds around $|n|$ times. So we get a picture like this (when $n=2$):
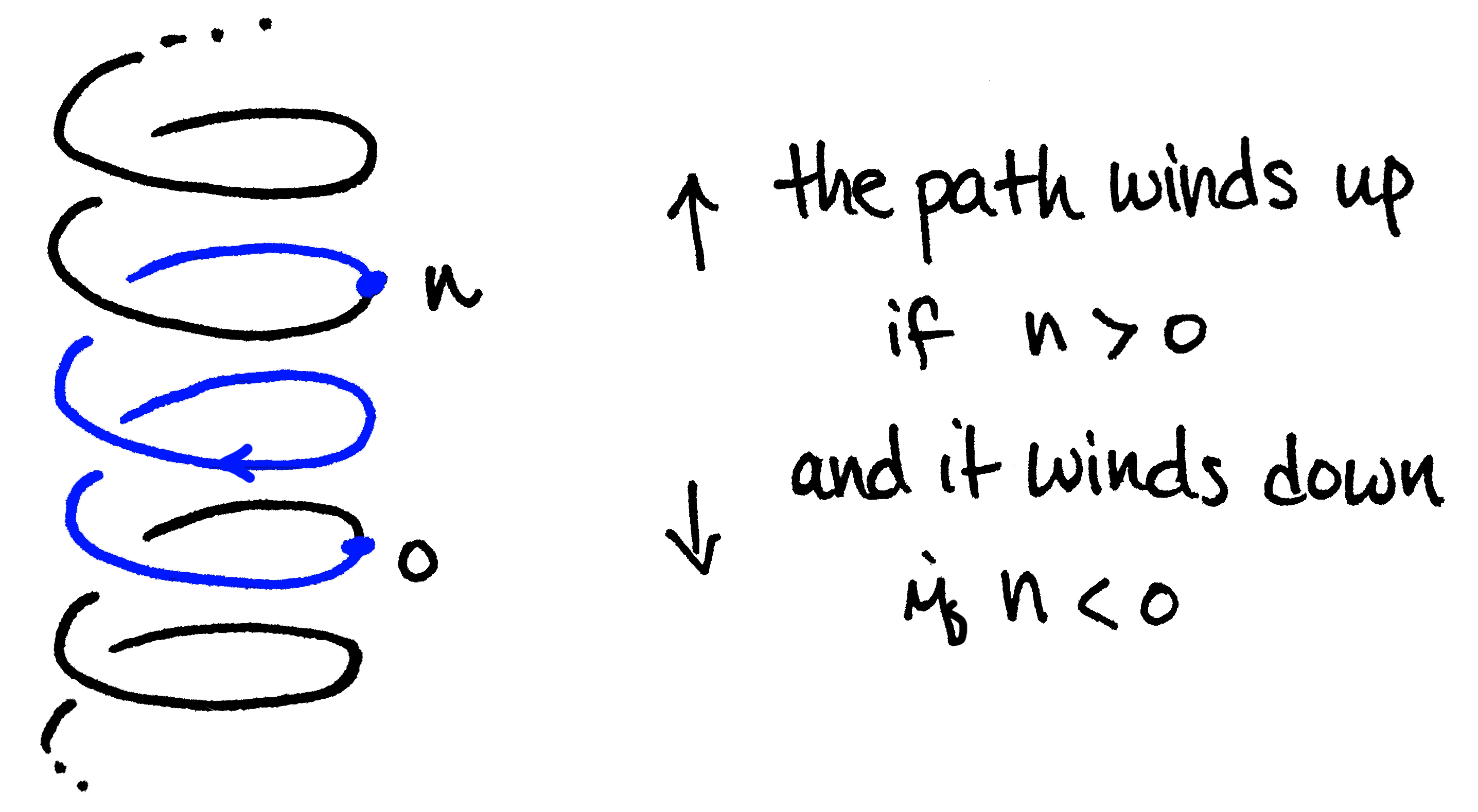
Next, define $\omega_n:I\to S^1$ to be the loop which sends $s\mapsto (\cos{2\pi ns},\sin{2\pi ns})$. Visually, $\omega_n(I)$ starts at $(1,0)$, wraps $|n|$ times around $S^1$ (clockwise if $n< 0$ and counterclockwise if $n>0$) and ends back at $(1,0)$. Here we pause to observe that $\omega_n=p\circ \widetilde{\omega}_n$ which allows us to write down the following commuting diagram:
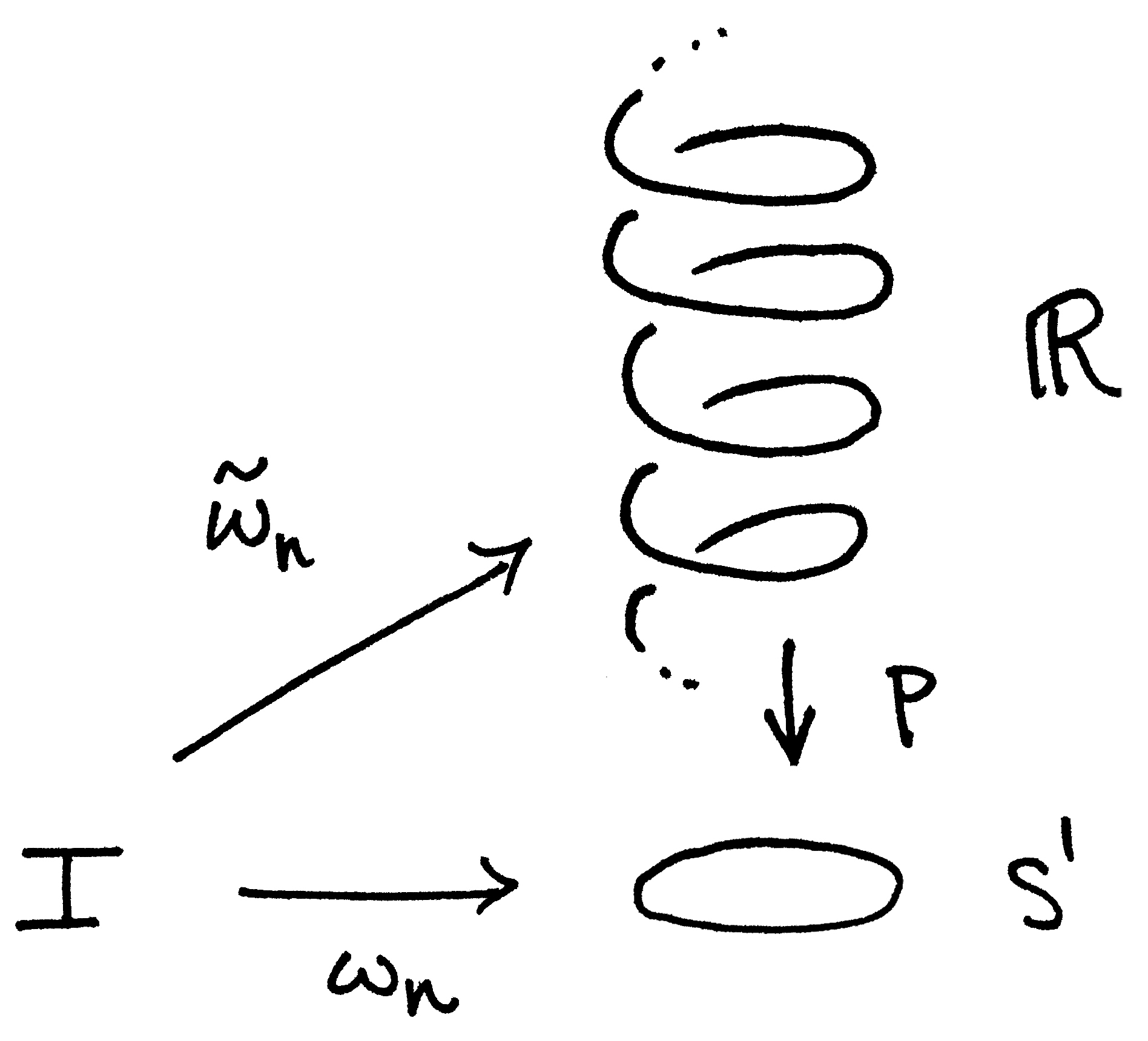
For this reason, we call $\widetilde{\omega}_n$ a lift of $\omega_n$. Finally, as a closing remark, notice that as the path $\widetilde{\omega}_n(I)$ climbs up/down the helix, its shadow, i.e. the projection $\omega_n$, winds around $S^1$. This correspondence beween the path in $\mathbb{R}$ and its shadow in $S^1$ is crucial to the proof, so I've included a couple of pictures to help the image 'stick.'
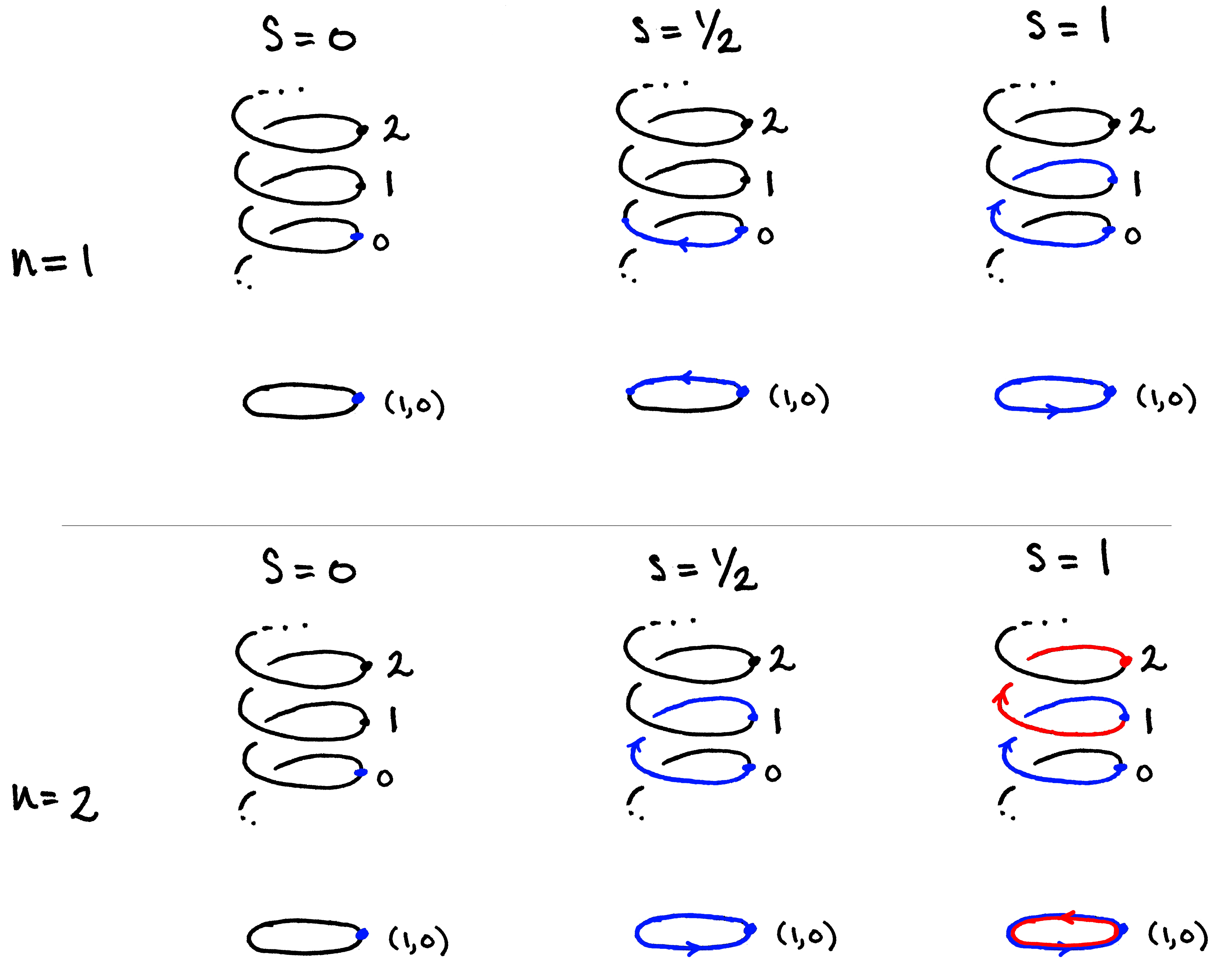
The following video illustrates the above rather nicely, especially the animation from 0:45 to 1:05. (After the 1:05 mark, the animation relates to covering spaces which we are not discussing in today's post.)

We are now ready to claim that the map defined by $\Phi:\mathbb{Z}\to\pi_1(S^1)$ by $n\mapsto [\omega_n]$ is a group isomorphism. Following the outline given in the introduction, we will prove next week that $\Phi$ is well-defined.
