The Fundamental Group of the Circle, Part 3

Welcome back to our proof that the fundamental group of the circle is isomorphic to $\mathbb{Z}$. Today's post is part 3 of our outline:
Part 1: Set-up/observations
Part 2: Show $\Phi$ is well defined
Part 3: Show $\Phi$ is a group homomorphism
Part 4: Show $\Phi$ is surjective
Part 5: Show $\Phi$ is injective (Note: parts 4 and 5 require two lemmas whose proofs we will defer until part 5)
Part 6: Prove the two lemmas used in parts 4 and 5
Last week we showed that the map map $\Phi:\mathbb{Z}\to\pi_1(S^1)$ by $n\mapsto[\omega_n]$ where $\omega_n:[0,1]\to S^1$ is the loop given by $s\mapsto (\cos{2\pi n s}, \sin{2\pi n s})$ is well-defined. Our goal for today is to show that it is indeed a group homomorphism.
Claim: Φ is a Homomorphism, i.e. Φ(m+n)=Φ(m)∙Φ(n)
Recall that $\omega_n=p\circ\widetilde{\omega}_n$ is a loop from $I$ to $S^1$ where $\widetilde{\omega}_n:I\to\mathbb{R}$ is a path (a straight line, actually) from $0$ to $n$.
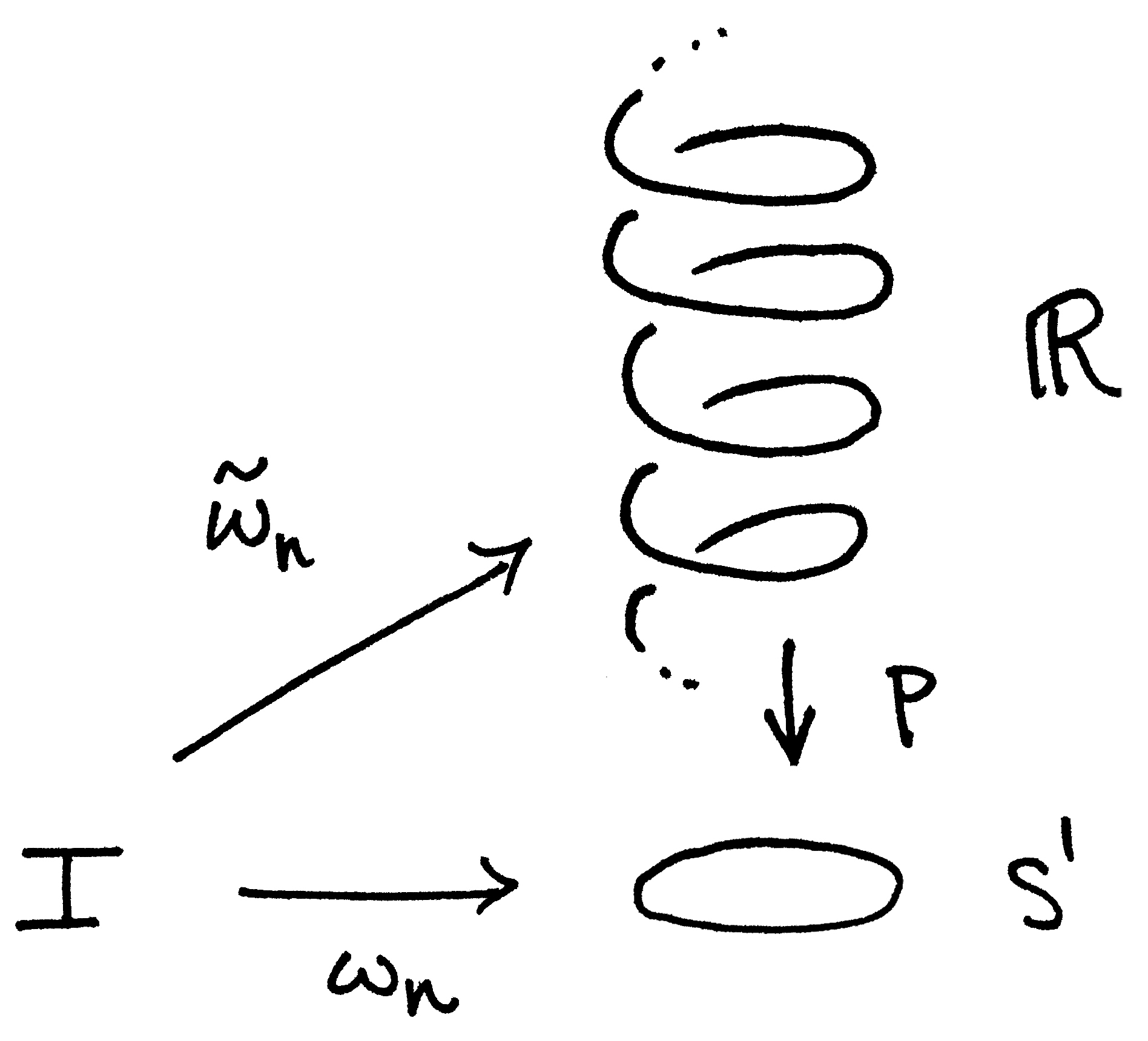

We begin by defining a translation map $\tau_m:\mathbb{R}\to\mathbb{R}$ by $x\mapsto x+m$ for $m\in\mathbb{Z}$. Notice that in our "helix model" of $\mathbb{R}$, this is a shift up or down by $|m|$. This observation lets us conclude that $$\widetilde{\omega}_m\cdot \tau_m \widetilde{\omega}_n\;\underset{F}{\simeq}\;\widetilde{\omega}_{m+n}$$ by some homotopy $F:I\times I\to\mathbb{R}$ in $\mathbb{R}$. This becomes evident once we pause for a bit to think about what these paths really are:
- On the right-hand side, $\widetilde{\omega}_{m+n}$ is simply the line (path) from $0$ to $m+n$ in $\mathbb{R}$
- On the left-hand side, $\widetilde{\omega}_m\cdot \tau_m \widetilde{\omega}_n$ is the product of the path from $0$ to $m$ (in $\mathbb{R}$) with the path from $m$ to $n+m$ (in $\mathbb{R}$). (Note: $\tau_m \widetilde{\omega}_n$ takes the line which starts at $0$ and ends at $n$ and shifts it so that the starting point is now $m$ and the ending point is now $m+n$.) In other words, it is the union of the green and blue paths below.
So we must have that $\widetilde{\omega}_{m+n}$ (the red path) and $\widetilde{\omega}_m\cdot \tau_m \widetilde{\omega}_n$ (the green/blue path) are homotopic - they are "basically the same"!

So when we project each of these paths onto $S^1$, we see that the resulting paths are also homotopic: $$p\circ(\widetilde{\omega}_m\cdot \tau_m \widetilde{\omega}_n)\underset{G}{\simeq}p\circ \widetilde{\omega}_{m+n}$$ where $G:I\times I\to S^1$ is $G=p\circ F$. And now we're basically done! We simply need to write down the following equalities:

So $\Phi$ is indeed a homomorphism. QED! Next week we'll move on to Part 4 by proving that $\Phi$ is surjective.
