Topology vs. "A Topology" (cont.)
This blog post is a continuation of today's episode on PBS Infinite Series, "Topology vs. 'a' Topology." My hope is that this episode and post will be helpful to anyone who's heard of topology and thought, "Hey! This sounds cool!" then picked up a book (or asked Google) to learn more, only to find those formidable three axioms of 'a topology' that, admittedly, do not sound cool.
But it turns out those axioms are what's "under the hood" of the whole topological business! So without further ado, let's pick up where we left off in the video.
How is this a topological space?
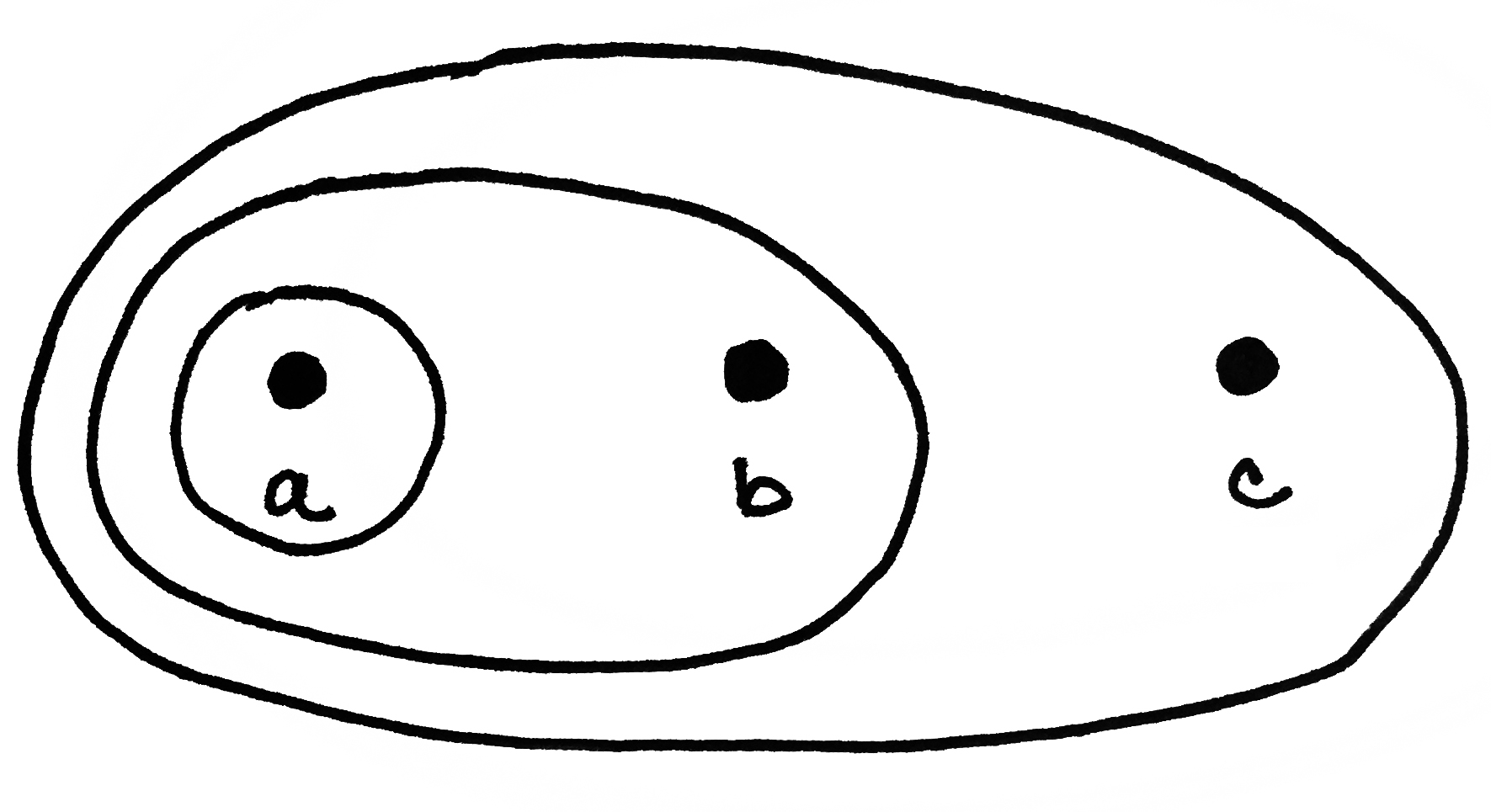
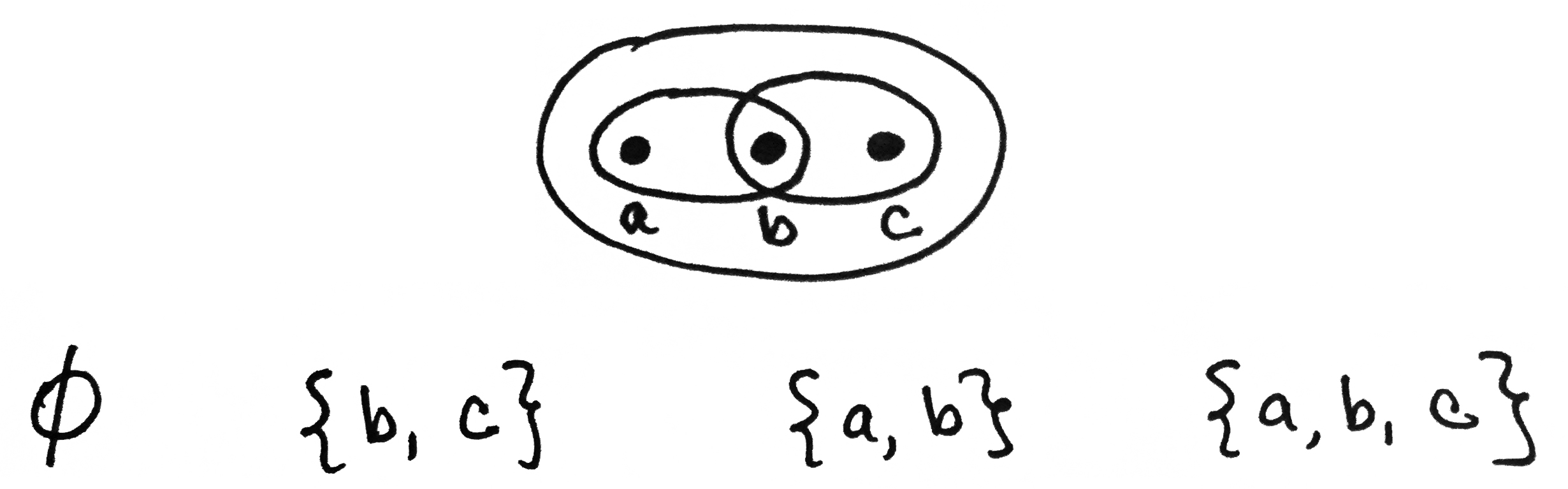
As mentioned in the video, a topological space is a set $X$ together with a collection of subsets that satisfy three axioms. Here we're looking at a set with three elements, $a,b$ and $c$. Let's list its elements like this: $X=\{a,b,c\}$. What's the deal with the circles/ovals? They're telling us what the open sets are! A subset is open if it has a circle/oval around it OR if it's the empty set. (It's hard to draw the empty set.) This means there are a total of four open sets.
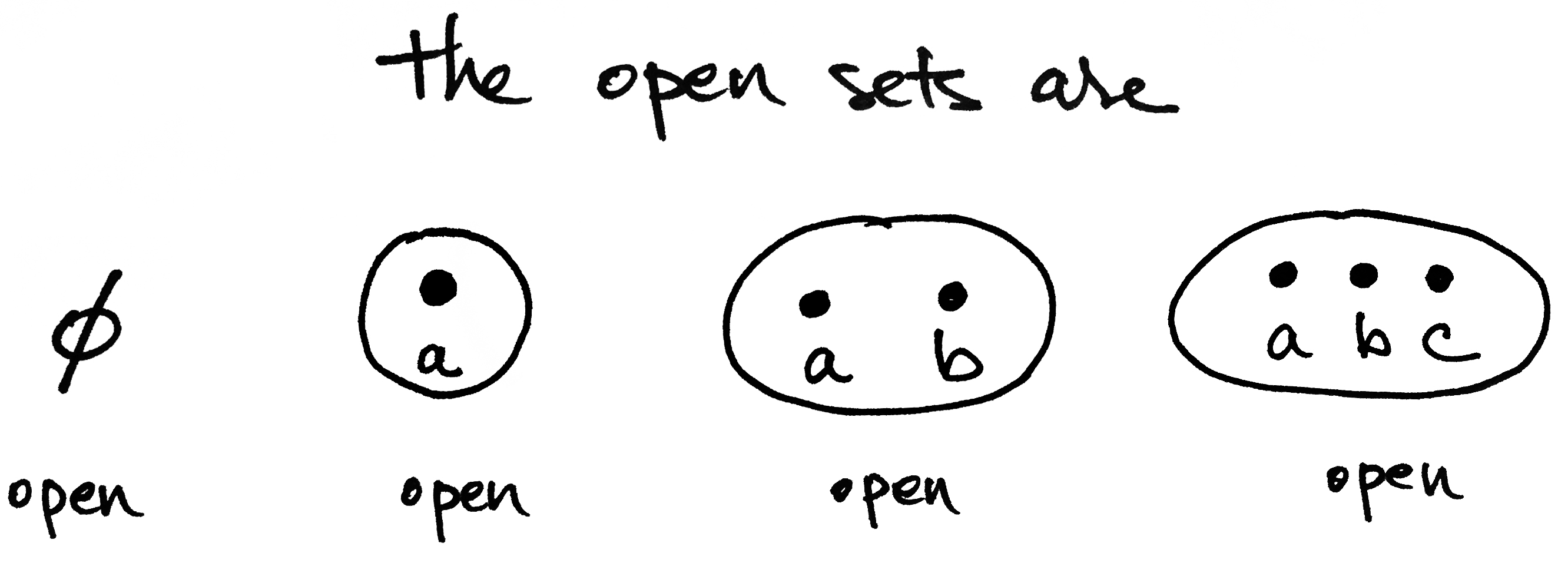
Notice the set on the far right is $X$ itself! Let's clean up the notation and use curly brackets instead of ovals.
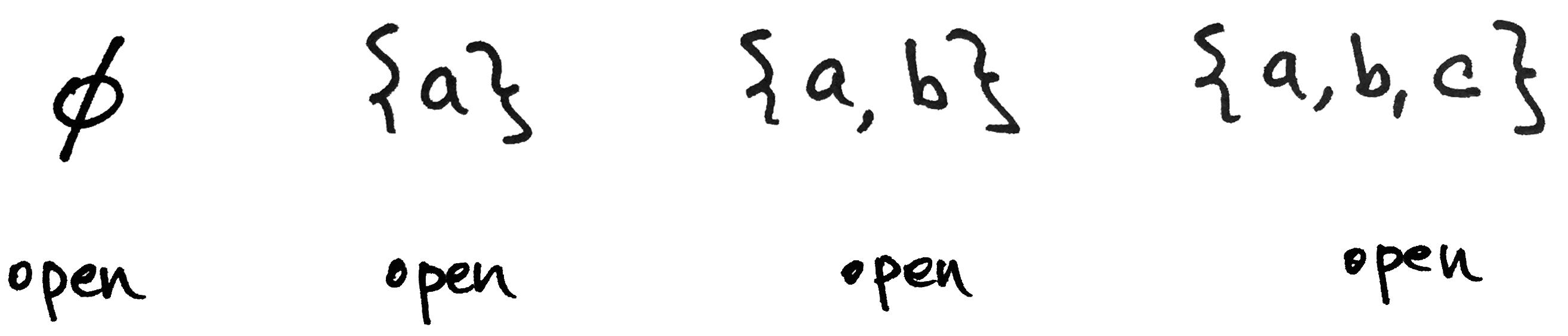
Now we just have to check that the three axioms hold. Let's do this one at a time.
Axiom #1: The set X and the empty set are open.
This one is quick to check. Are $X=\{a,b,c\}$ and $\varnothing$ in our list of open sets? YES. Therefore Axiom #1 holds. Done and done.
Axiom #2: Any union of open sets is open.
To check this, we should form all possible unions of the four open sets, and verify that the result is a set in the list above. For example, is $\{a\} \cup\{a,b\}$ an open set? YES! It equals $\{a,b\}$ which is in the list above. It turns out that's the only thing we really have to check. Other unions involve $X$ and $\varnothing$. But checking those is easy because of the following facts:

Conclusion? Axiom #2 is satisfied.
Axiom #3: any finite intersection of open sets is open.
To check this, we should form all possible intersections of the four open sets, and verify that the result is a set in the list. For example, Is $\{a\}\cap\{a,b\}$ an open set? YES! It equals $\{a\}$ which is in the list above. Again, it turns out that's the only thing we really need to check because of the following helpful facts:

So Axiom #3 is satisfied. (By the way, the word "finite" in Axiom #3 is redundant in this example because we only have 4 open sets to check. "Finiteness" plays a bigger role when you have infinitely many open sets to deal with.) Voila! All three axioms are satisfied, therefore the collection of open sets does form a topology on $X$. This means that the set $\{a,b,c\}$ - together with the four open sets - form a topological space.By the way, I mentioned in the video that it's possible to define many different topologies on the same set. In the example above, we investigated just one, but it turns out there are 28 more we could have considered! In other words, there are 29 different ways to define a topology on a set with three elements. Nine of them are shown below.
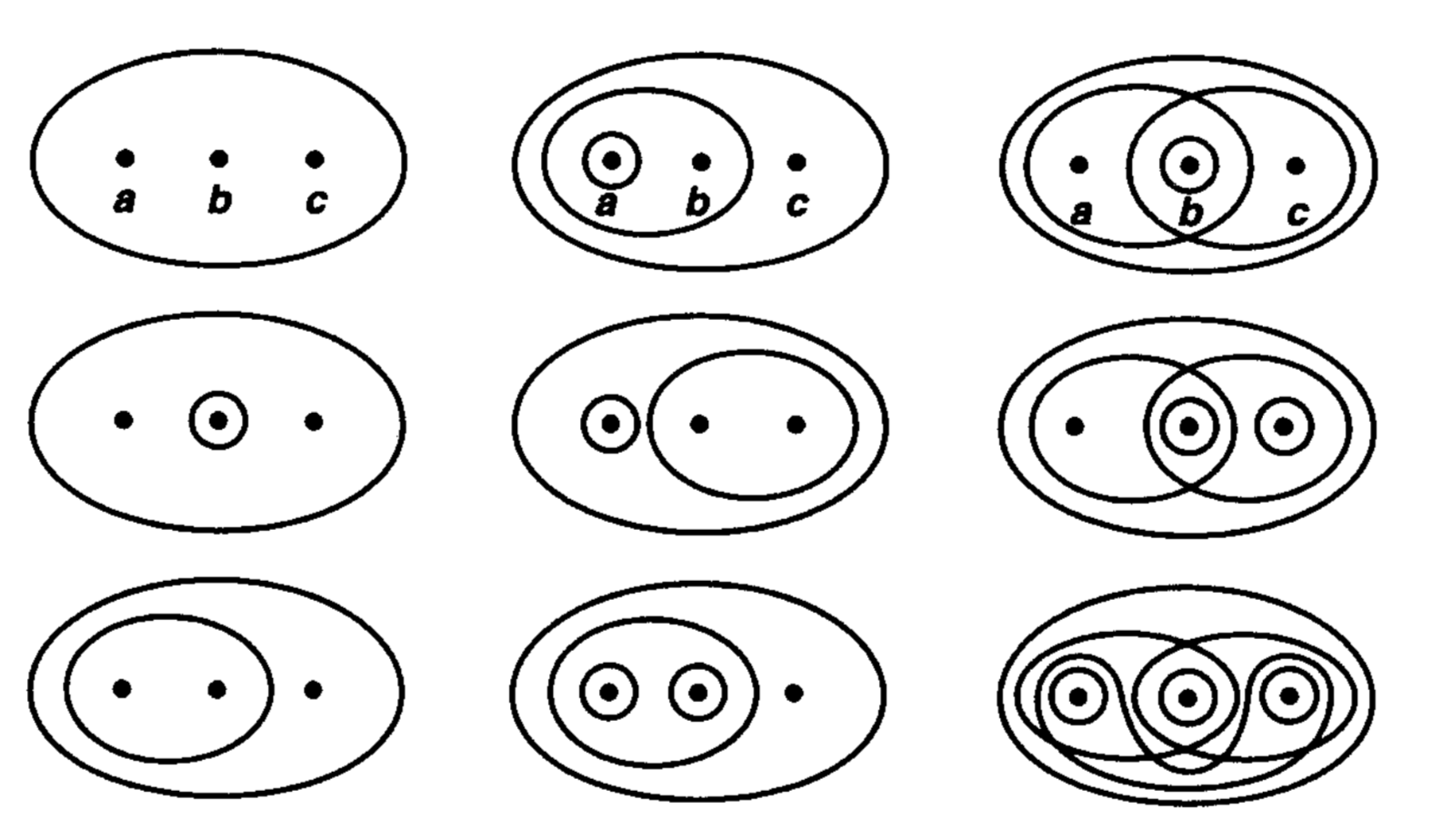
So here's something fun to think about: How many different topologies are there on a set with two elements?

So what's NOT a topological space?
Suppose we replace the set $\{a\}$ with $\{b,c\}$. Then the four subsets of sets of $X=\{a,b,c\}$ are
And this FAILS to be a topology! In particular, Axiom #3 is not satisfied: the intersection of $\{b,c\}$ and $\{a,b\}$ is $\{b\}$, which is NOT in the list above.
So now that you know what a topology is and what it isn't...
Here's the episode's challenge question!
Is THIS a topology on the set with 3 elements? Why or why not?

To enter the challenge, send me your ideas at pbsinfiniteseries@gmail.com. A correct solution will be chosen at random to receive a PBS Digital Studios t-shirt!

So topology's all about checking axioms? That's it?!
No way! The axioms are merely a springboard for "rubber sheet geometry." By abstracting the notion of openness, we can now make sense of continuity in a way that's more general than what you might learn in a calculus class. Continuity is an essential ingredient to the bending, twisting, and stretching -- but not tearing-- of shapes that you hear about. The "no tearing" part is precisely what continuity means. And continuity is defined in terms of open sets!
Once you embark on an exploration of topological spaces, you discover things like a surface with only one side or the fact that it's possible to turn your pants inside out without taking your feet off the ground. On the applied side, topology is used in neuroscience, data analysis and signal processing, fluid dynamics, string theory (see also here), and topological quantum field theory, just to name a few. And topological ideas permeate the pure math world, too. You can even use topology to prove that there are infinitely many primes!
And it all starts with three little axioms.
