Need Some Disjoint Sets? (A Measure Theory Trick)
Here's a quick "trick" that arises early on in a study of measure theory:
Trick: Given a countable collection of measureable sets $E_1,E_2,\ldots$ in some set $X$, consider their union $\bigcup_{i=1}^\infty E_i$. There exists an algorithm which allows us to create a new countable collection of measurable sets $F_1,F_2,\ldots$ such that the $F_i$ are pairwise disjoint and have the same union as the original, i.e. $\cup_i F_i = \cup_i E_i$.
Here's how:
- Step 1: Given $\{E_i\}_{i=1}^\infty$, set $F_1=E_1$.
- Step 2: For each $i>1$, define $F_i=E_i\smallsetminus \bigcup_{j=1}^{i-1}E_j$.
- Step 3: Observe that the $F_i,F_j$ are pairwise disjoint and that $\bigcup_{i=1}^{\infty}E_i=\bigcup_{i=1}^{\infty}F_i$. Voila!
To illustrate, suppose we have five sets: $E_1$ through $E_5$, represented by the five (very lopsided) "ovals" below. Then:
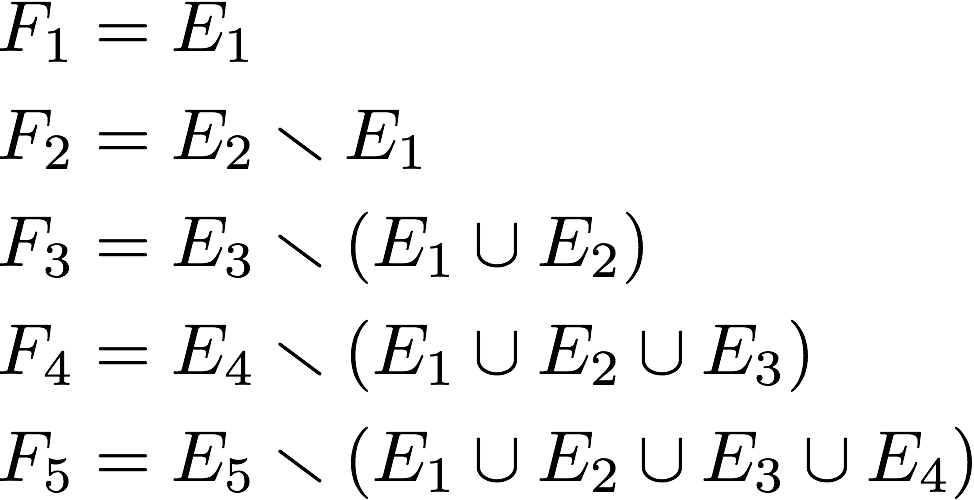
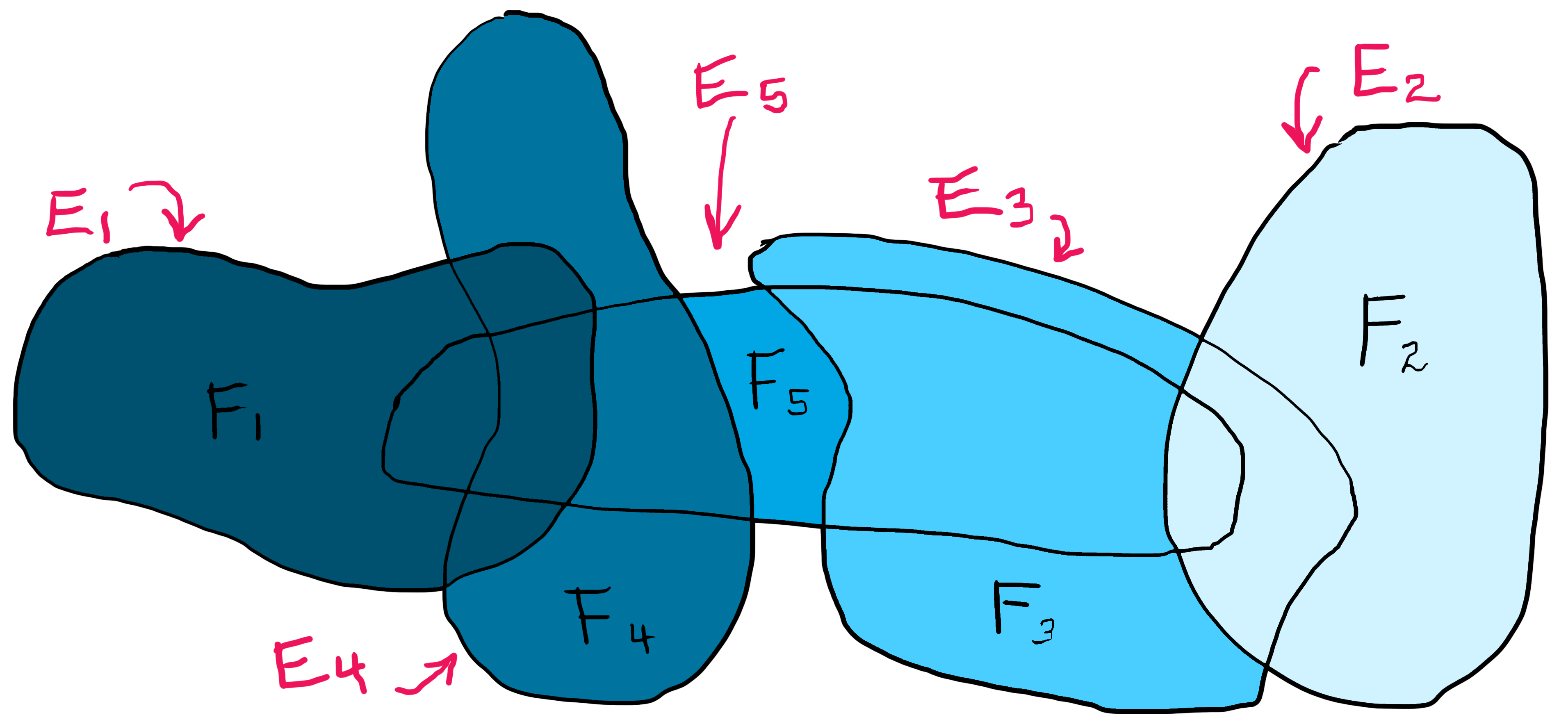
Each shade of blue represents one of the $F_i$, showing they are indeed disjoint. Also, their union $\bigcup_{i=1}^5 F_i$ is equal to $\bigcup_{i=1}^5 E_i$ as claimed.
As far as application goes, one place you might find this little trick is in the proof that if $X$ is a measure space with measure $\lambda$, then $\lambda$ is continuous from below. That is, if $\{E_i\}_{i=1}^\infty\subset X$ is a collection of measurable sets such that $E_1\subset E_2\subset\cdots$, then $$\lambda\left(\bigcup_{i=1}^\infty E_i\right)=\sum_{i=1}^\infty \lambda(E_i).$$

Side Comment: This trick is almost like the "measure theory version" of the Gram-Schmidt Process from linear algebra!
Gram-Schmidt: If $\mathscr{A}=\{v_1,\ldots,v_n\}$ is a set of linearly independent vectors in some vector space $V$, then there is an algorithm which converts $\mathscr{A}$ to an orthonormal set (so the $v_i$, $v_j$ are "disjoint" in the sense that their inner product is zero) with the same span (i.e. the new collection of vectors has the same "cover" as the original).
