A Little Fact From Group Actions

‍

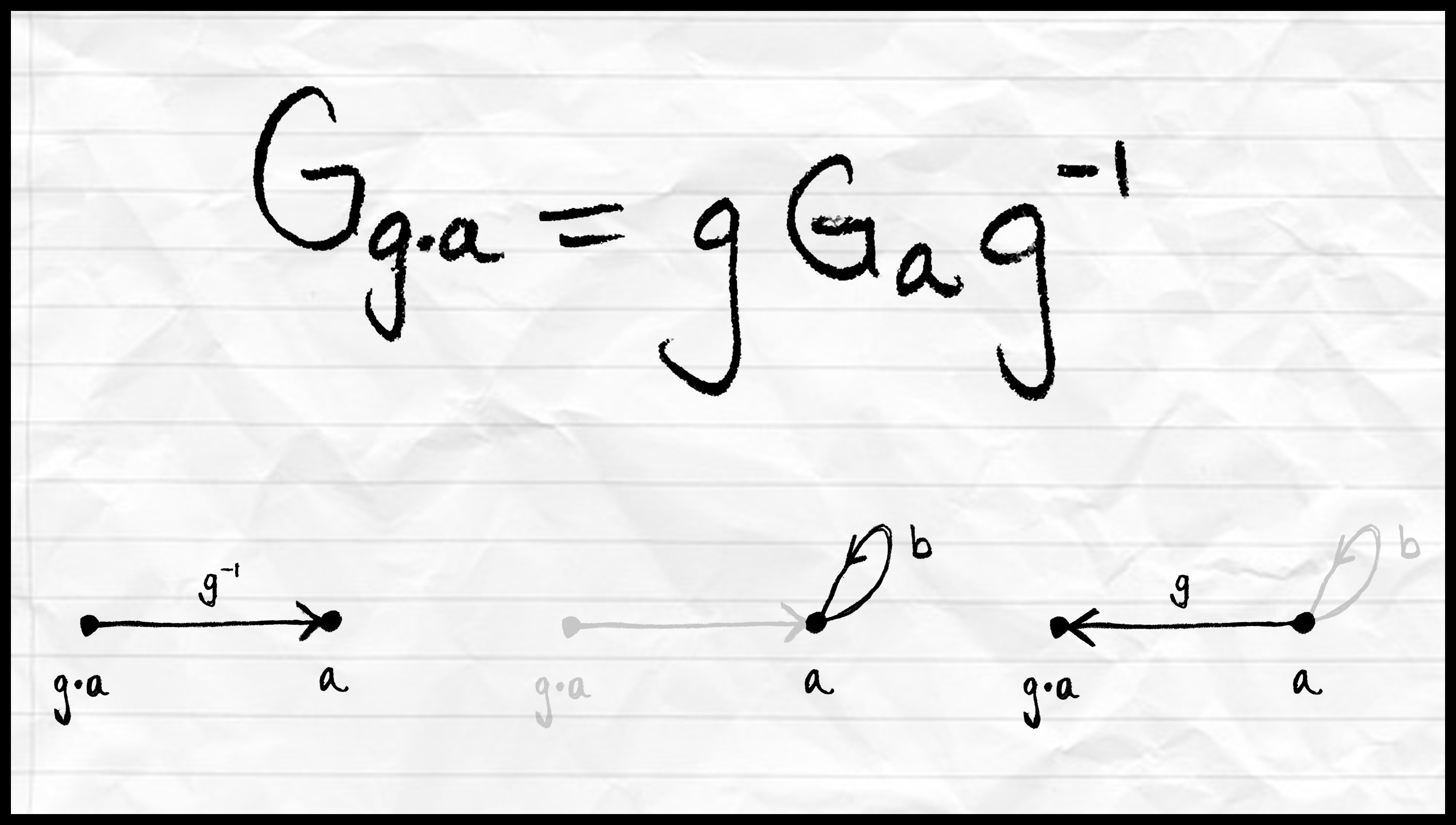
Today we've got a little post on a little fact relating to group actions. I wanted to write about this not so much to emphasize its importance (it's certainly not a major result) but simply to uncover the intuition behind it.

Let a group $G$ act on a set $A$. We define the stabilizer of an element $a\in A$ to be the set of all elements in $G$ which fix (stabilize) $a$ and denote it by $G_a$: $$G_a=\{g\in G:g\cdot a=a\}.$$ It's a fact that $$G_{g\cdot a}=g G_a g^{-1}$$ which is to say, "the stabilizer of $g\cdot a\in A$ equals the conjugate by $g\in G$ of the stabilizer of $a\in A$." Now, if you're like me, you've got two looming questions: What? and Why? 

‍

What?

The equality above answers the question, "How can I fix an element in $A$ that has already been moved around by some element in $G$?" In other words, you're given $a\in A$ and you let $G$ shuffle all the elements of $A$ so that the little $a$ moves to another element $g \cdot a$. Now suppose you have $G_a$ at your disposal, i.e. you know how to fix $a$. But suppose you want to know how to fix the new guy $g\cdot a$. How would you do it? Here's how:

‍

Step 1: Send $g\cdot a$ back to $a$ by letting $g^{-1}$ act:

Step 2: Fix $a$ by letting any $b\in G_a$ act:

Step 3: Send $a$ back to $g\cdot a$ by letting $g$ act:

‍

And there you have it! The element $gbg^{-1}$ with $b\in G_a$ fixes $g\cdot a$. That's all that's going on here. With this intuition in mind, let's prove it formally (i.e. answer the question Why?). 

‍

Why?

As usual, we prove the equality $G_{g\cdot a}=g G_a g^{-1}$ by showing containment both directions. To begin let $b\in G_a$ so that $b\cdot a=a$. We wish to show $gbg^{-1}\in G_{g\cdot a}$. But this is immediate: $$gbg^{-1}\cdot(g\cdot a)= (gbg^{-1}g)\cdot a = (gb)\cdot a=g\cdot (b\cdot a)=g\cdot a.$$ Since $gbg^{-1}$ fixes $g\cdot a$ it follows that $gbg^{-1}\in G_{g\cdot a}$ and so $gG_ag^{-1}\subseteq G_{g\cdot a}$.

For the other direction, we'll use a little trick. Let $h=g\cdot a$ so that $a=g^{-1}\cdot h$. Then by the above paragraph we know   $$g^{-1}G_hg\subseteq G_{g^{-1}\cdot h}.$$ But the left hand side is equal to $g^{-1}G_{g\cdot a}g$, and the right hand side is equal to $G_a$. Hence $g^{-1}G_{g\cdot a}g\subseteq G_a$ and therefore $G_{g\cdot a}\subseteq g G_a g^{-1}$.

‍

QED!