A Non-Measurable Set

Today we're looking at a fairly simple proof of a standard result in measure theory. In what follows, let $\lambda$ denote the Lebesgue measure on $\mathbb{R}$.
Theorem: Any measurable subset $A\subset \mathbb{R}$ with $\lambda(A)>0$ contains a non-measurable subset.
(Remark: we used this theorem last week to prove the existence of a Lebesgue measurable set which is not a Borel set.)
Proof
It suffices to assume $A\subset (0,1)$.
Why? Because if $A\subset\mathbb{R}$ has postive measure, then there is some $n\in\mathbb{Z}$ such that $A\cap(n,n+1)$ also has positive measure, and thus, by translation invariance, so does $A'=A\cap(n,n+1)-n\subset (0,1)$. So if $N\subset A'$ is a non-measurable set, then $N+n\subset A\cap (n,n+1)\subset A$ is our desired non-measurable set.
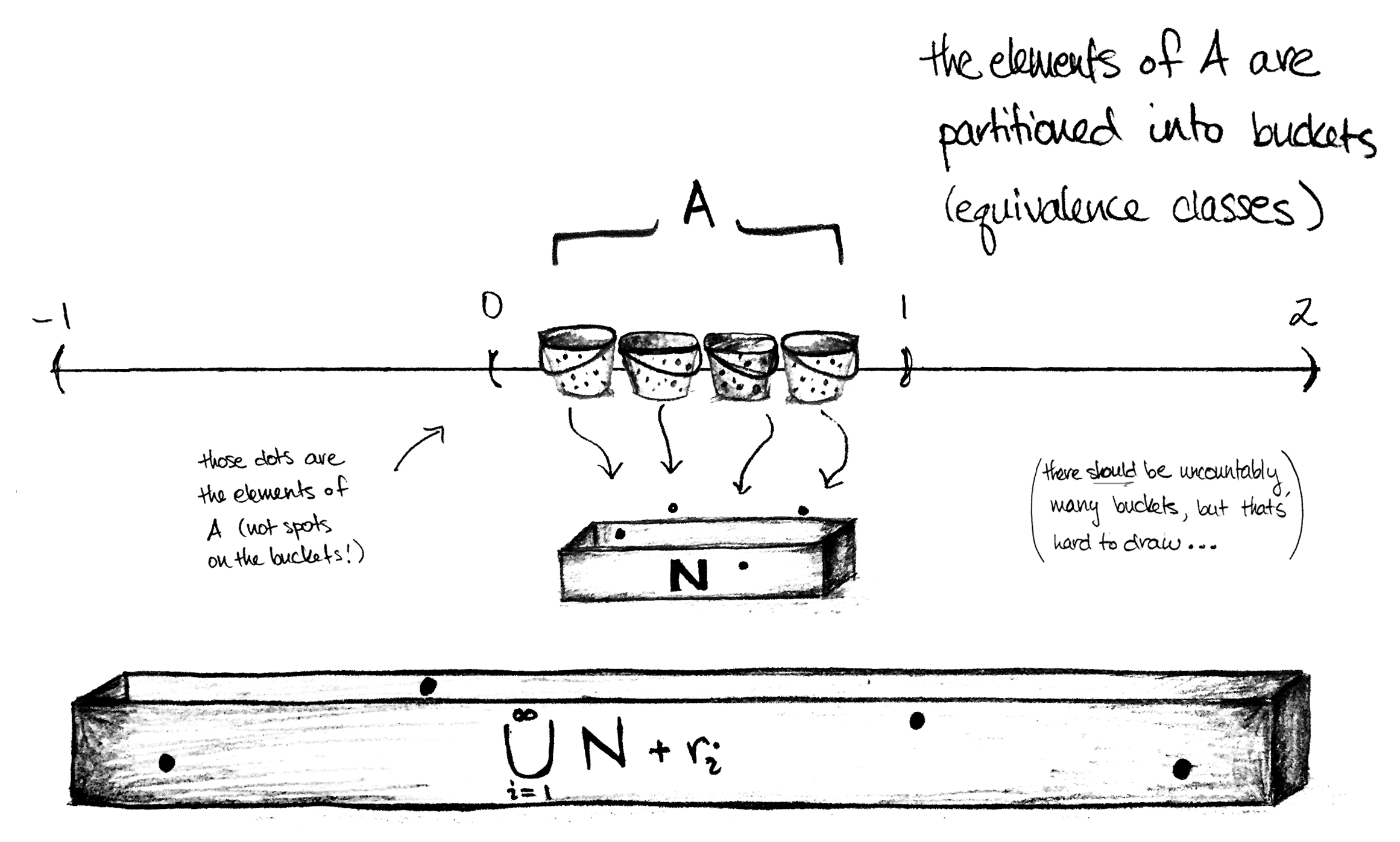
Step 1: Define an equivalence relation
Define an equivalence relation on $\mathbb{R}$ by $r\sim s$ whenever $r-s\in\mathbb{Q}$. Since $A\subset\mathbb{R}$, the elements of $A$ are partitioned by this relation.
Step 2: Apply the Axiom of Choice
By the Axiom of Choice*, let $N\subset A$ be the subset consisting of one member from each equivalence class and assume $N$ is measurable.
Step 3: Show λ(A) must equal 0 (a contradiction)
First notice that we can cover $A$ by a pairwise disjoint union of sets: $$A\subset\bigcup_{r\in(-1,1)\cap\mathbb{Q}}N+r.$$ Proof that the union covers $A$: This follows from the fact that each element of A lies in an equivalence class. Indeed, let $a\in A$. Then there is some $n_a\in N$ so that $a\sim n_a$ which means there is an $r\in\mathbb{Q}$ such that $a-n_a=r$. In particular $r$ must lie within $(-1,1)$ since $a,n_a\in(0,1)$!** Thus $a=n_a+r\in N+r$. Since $a$ was arbitrary, we conclude $A\subset\cup_r N+r$.
Proof that the union is disjoint: This is follows from the fact that $N$ contains exactly one element from each equivalence class. Explicitly: Suppose to the contrary that there exist distinct $r,s\in(-1,1)\cap\mathbb{Q}$ such that $N+r\cap N+s\neq \varnothing$. Then there are $n_1,n_2\in N$ satisfying $n_1+r=n_2+s$ and so $n_1-n_2=r-s\in\mathbb{Q}$ which means $n_1\sim n_2$. It follows by definition of $N$ that $n_1=n_2$ and hence $r=s$, a contradiction.
Now let $\{r_i\}_{i=1}^\infty$ be an enumeration of the rationals in $(-1,1)$. From what we've just shown, we can write \begin{align*} \lambda(A)&\leq \lambda\left(\bigcup_{i=1}^\infty N+r_i \right) \\ &=\sum_{i=1}^\infty \lambda (N+r_i)\\ &=\sum_{i=1}^\infty \lambda(N) \end{align*} where in the last line we have used the fact that Lebesgue measure is translation invariant. But (!) since $-1< r_i < 1$ for all $i$ and since $N\subset (0,1)$, we know that $N+r_i$ must be contained within $(-1,2)$ for each $i$ and hence $$\bigcup_{i=1}^\infty N+r_i\subset (-1,2).$$ So by monotonicity of Lebesgue measure, $\displaystyle{\sum_{i=1}^\infty \lambda(N+r_i)} \leq \lambda((-1,2))=3$. Together with the inequalities a few lines above this implies $$\lambda(A)\leq \sum_{i=1}^\infty \lambda(N)\leq 3.$$ The only way this last inequality can hold is if $\lambda(N)=0.$*** Hence $$\lambda(A)\leq \sum_{i=1}^\infty\lambda(N)=0$$ which is a contradiction. Thus, our assumption that $N$ is measurable is wrong.

Footnotes:
* The Axiom of Choice says that if we have a collection of sets $S_1,S_2,S_3,\ldots$ (not necessarily countable, but you get the idea), then we can form a new collection $\{x_1,x_2,x_3,\ldots\}$ where $x_i\in S_i$ for each $i$. That is, we can take one element $x_i$ from each set $S_i$ and form a new set of "representatives", if you will.
** For example, we might have $a=0.001$ and $n_a=0.99$ so that $a-n_a=-0.989$. Or we could have $a=0.8$ and $n_a=0.01$ so that $a-n_a=0.79$.
*** Otherwise, if $\lambda(N)$ is equal to some positive number $c$, then we have $c\cdot\sum_{i=1}^\infty=\infty \leq 3$ which is not true.
