On Connectedness, Intuitively
Today's post is a bit of a ramble, but my goal is to uncover the intuition behind one of the definitions of a connected topological space. Ideally, this is just a little tidbit I'd like to stash in The Back Pocket. But as you can tell already, the length of this post isn't so "little"! Oh well, here we go!
We say a topological space $X$ is connected if it is not disconnected, i.e. if it cannot be written as $X=A\cup B$ where $A$ and $B$ are disjoint, nonempty open subsets of $X$. This seems intuitive enough, right? We can easily visualize a disconnected space. But there's also an equivalent definition:
$X$ is connected if every continuous function $f:X\to\{0,1\}$ is constant, where $\{0,1\}$ has the discrete topology.*

At first glance, you might think How in the world are these equivalent? Although the proof isn't too hard, it may be difficult to see the connection (har har) intuitively. But I claim that this second definition of connectedness is just as intuitive as the first! Hopefully by the end of this post, you'll agree.
What's Really Going on Here?
To say "there is a continuous function from $X$ to $\{0,1\}$" is the mathematician's way of saying "$X$ and $\{0,1\}$ share the same structure." Indeed, what's characteristic about a disconnected space? It's made up of two pieces! (Loosely speaking.) And what's the simplest example of a set which is made up of two pieces? $\{0,1\}$ of course! (Why? Because, well, it's made up of two pieces.) So if we can find a structure preserving map $f$ (a continuous function) from $X$ to $\{0,1\}$ which is not constant, then some elements of $X$ are mapped to $0$ while others are mapped to $1$. Hence we can separate the elements of $X$ into two subsets by putting a label, either a $0$ or a $1$, on each element. That's what a function does! If you like, imagine that $f$ paints all the elements that map to $0$ red and all the elements that map to $1$ blue. Then we'll have this scenario:
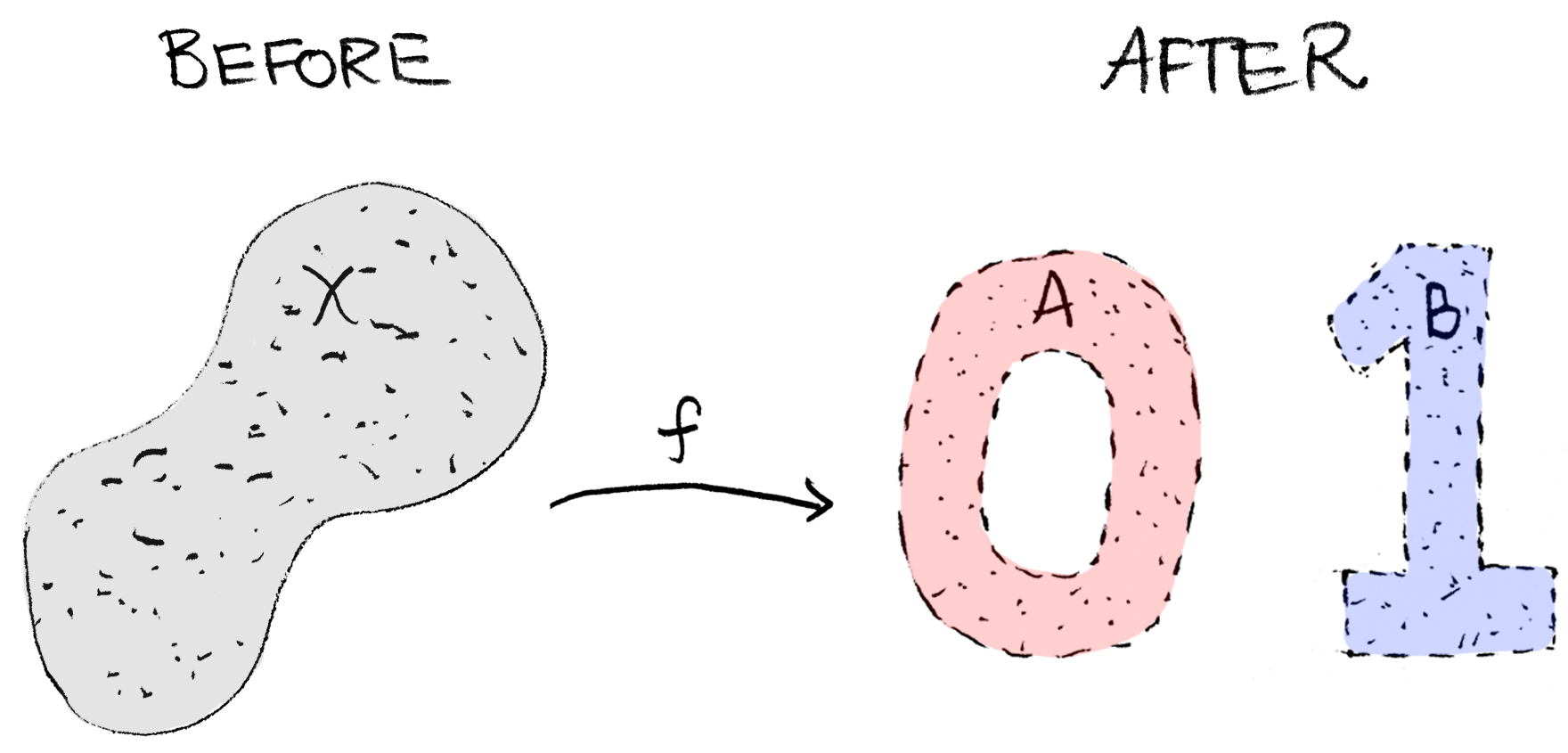
and this is precisely what it means for $X$ to be disconnected! On the other hand, if every continuous function assigns to all elements in $X$ a single value** in $\{0,1\}$ (or a single color, either red or blue), then it must be that $X$ itself is intrinsically a single unit, that is, $X$ is connected.
This observation is really a consequence of the fact that continuity preserves connectedness. You know the theorem:
If $f:X\to Y$ is a continuous map between topological spaces $X$ and $Y$, and if $X$ is connected, then $f(X)$ is connected.
In particular, consider the special case when $Y=\{0,1\}$. If we can find a continuous function $f:X\to\{0,1\}$ such that $f(X)\subset\{0,1\}$ is not connected, then by the above we may conclude that $X$ is not connected either. But what does it mean for $f(X)\subset\{0,1\}$ to be "not connected"? It means that $f(X)$ can be written as a union of two nonempty, disjoint, open subsets of $\{0,1\}$. The only* possibility for this is if $f(X)=\{0\}\cup\{1\}$! And this is precisely what it means to say $f:X\to\{0,1\}$ is not constant, which ties back to our illustration above. To put it succinctly, the connectedness (or disconnectedness) of $X$ is reflected in the connectedness (or disconnectedness) of its image, $f(X)$.
Some Final Remarks
This idea of having a map between two objects which share similar properties is a recurring notion in math. Take group theory, for example. We expect to find an isomorphism between $\mathbb{Z}_2\times\mathbb{Z}_2$ and the Klein four group because they share the same structure. We also expect to find an isomorphism between $S_3$ and $\mathbb{Z}_3\rtimes\mathbb{Z}_2$ because they share the same structure. Similarly we expect there to be an isomorphism between $\mathbb{Z}$ and any infinite cyclic group because, well, they have the same structure! So you see? Continuous functions, just like homomorphisms, are simply tools which allow us to determine when two objects share the same properties. (And by the way, this isn't the first time we've seen an analogy between algebra and topology!) Now this observation may incline you to think, "Aha! So continuous functions between topological spaces are the analogue of isomorphisms between algebraic structures?" And the answer is "Almost." The observation is correct if you replace "continuous functions" by "homeomorphisms." (A homeomorphism is a bijective continuous function whose inverse is also continuous.) Here's the cool thing: the analogy between these two types of maps is no mere coincidence; it's all solidified via the language of category theory! But perhaps we'll save that discussion for another day.

Footnotes
* To say "$\{0,1\}$ has the discrete topology" means that the open sets of $\{0,1\}$ are $\varnothing,\{0\},\{1\},$ and $\{0,1\}$.
**This is what it means for $f:X\to\{0,1\}$ to be constant, either all of $X$ gets sent to $0$ or all of $X$ gets sent to $1$.
