Operator Norm, Intuitively

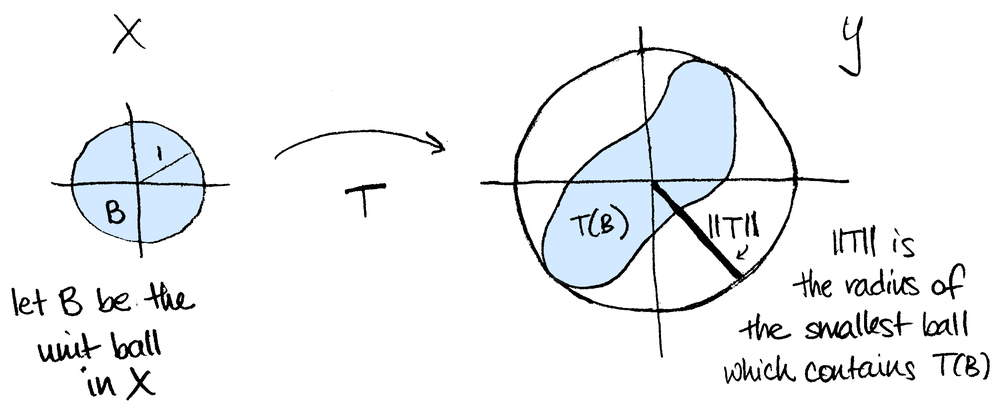
If $X$ and $Y$ are normed vector spaces, a linear map $T:X\to Y$ is said to be bounded if $\|T\| <\infty$ where $$\|T\|=\sup_{\underset{x\neq 0}{x\in X}}\left\{\frac{|T(x)|}{|x|}\right\}.$$ (Note that $|T(x)|$ is the norm in $Y$ whereas $|x|$ is the norm in $X$.) One can show that this is equivalent to $$\|T\|=\sup_{x\in X}\{|T(x)|:|x|=1\}.$$ So intuitively (at least in two dimensions), we can think of $\|T\|$ this way: