Lebesgue Measurable But Not Borel
The Basic Idea
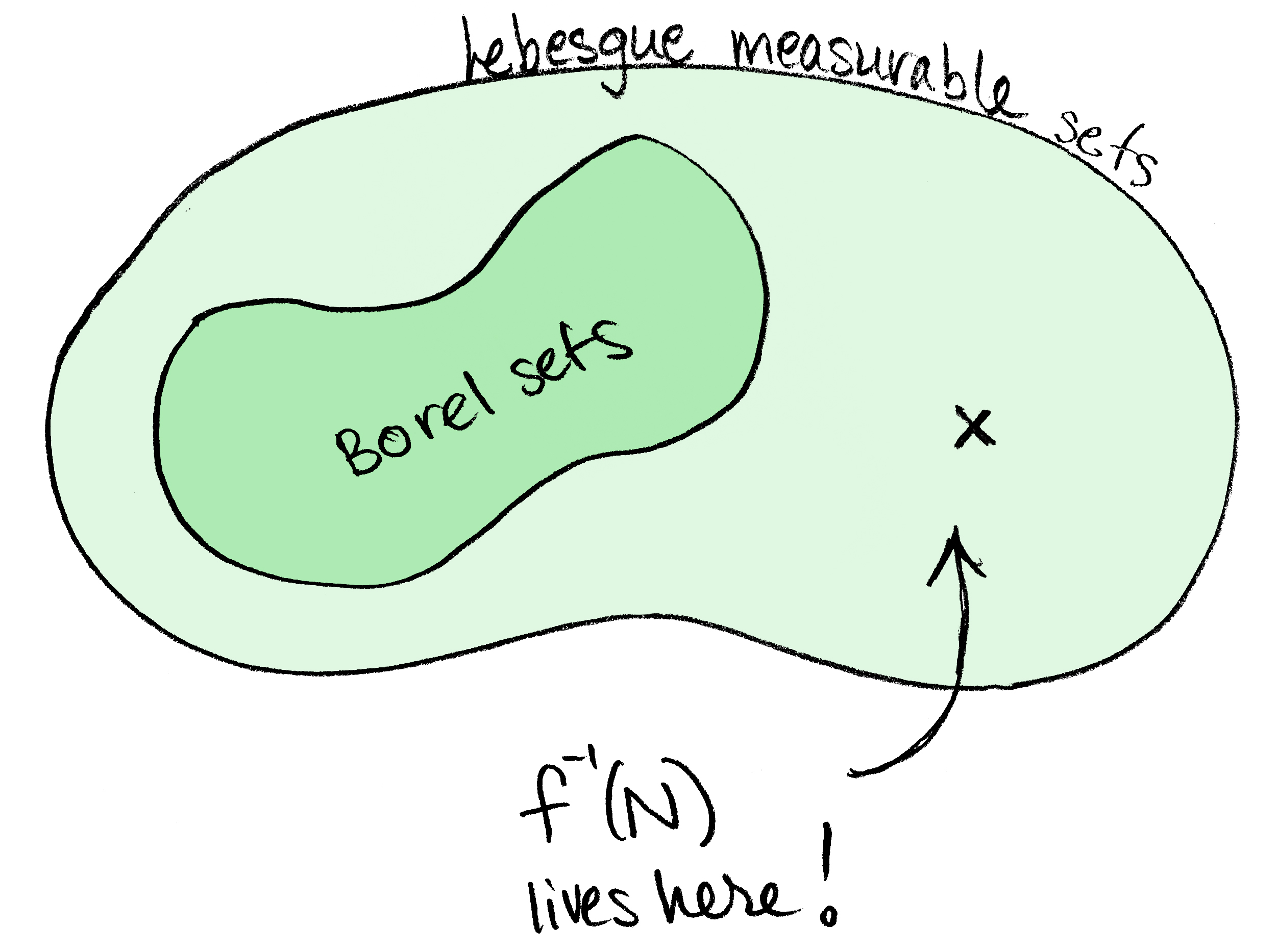
Our goal for today is to construct a Lebesgue measurable set which is not a Borel set. Such a set exists because the Lebesgue measure is the completion of the Borel measure. (The collection $\mathscr{B}$ of Borel sets is generated by the open sets, whereas the set of Lebesgue measurable sets $\mathscr{L}$ is generated by both the open sets and zero sets.) In short, $\mathscr{B}\subset \mathscr{L}$, where the containment is a proper one.
To produce a set in $\mathscr{L}\smallsetminus \mathscr{B}$, we'll assume two facts:
- Every set in $\mathscr{L}$ with positive measure contains a non (Lebesgue) measurable subset.
- 97.3% of all counterexamples in real analysis involve the Cantor set.
Okay okay, the last one isn't really a fact, but it may not surprise you that the Cantor set is central to today's discussion. In summary, we will define a homeomorphism (a continuous function with a continuous inverse) from $[0,1]$ to $[0,2]$ which will map a (sub)set (of the Cantor set) of measure 0 to a set of measure 1. By fact #1, this set of measure 1 contains a non-measurable subset, say $N$. And the preimage of $N$ will be Lebesgue measurable but will not be a Borel set. We'll fill in the details below, and while we do, keep in mind that we must work with a homeomorphism - a merely continuous function just won't do. And by playing with the Cantor set, we'll see that homeomorphisms (much less continuous functions!) don't always preserve measure. It's because of this that we can produce a Lebesgue measurable set which is not Borel.
From English to Math
Begin by defining a function $f:[0,1]\to[0,2]$ by $$f(x)=c(x)+x$$ where $c:[0,1]\to[0,1]$ is the Cantor function. The graph of $f$ looks much like that of $c$, except the horizontal lines are now all tilted with a slope of 1. I've drawn the graph for the first two iterations. This function has the following properties:
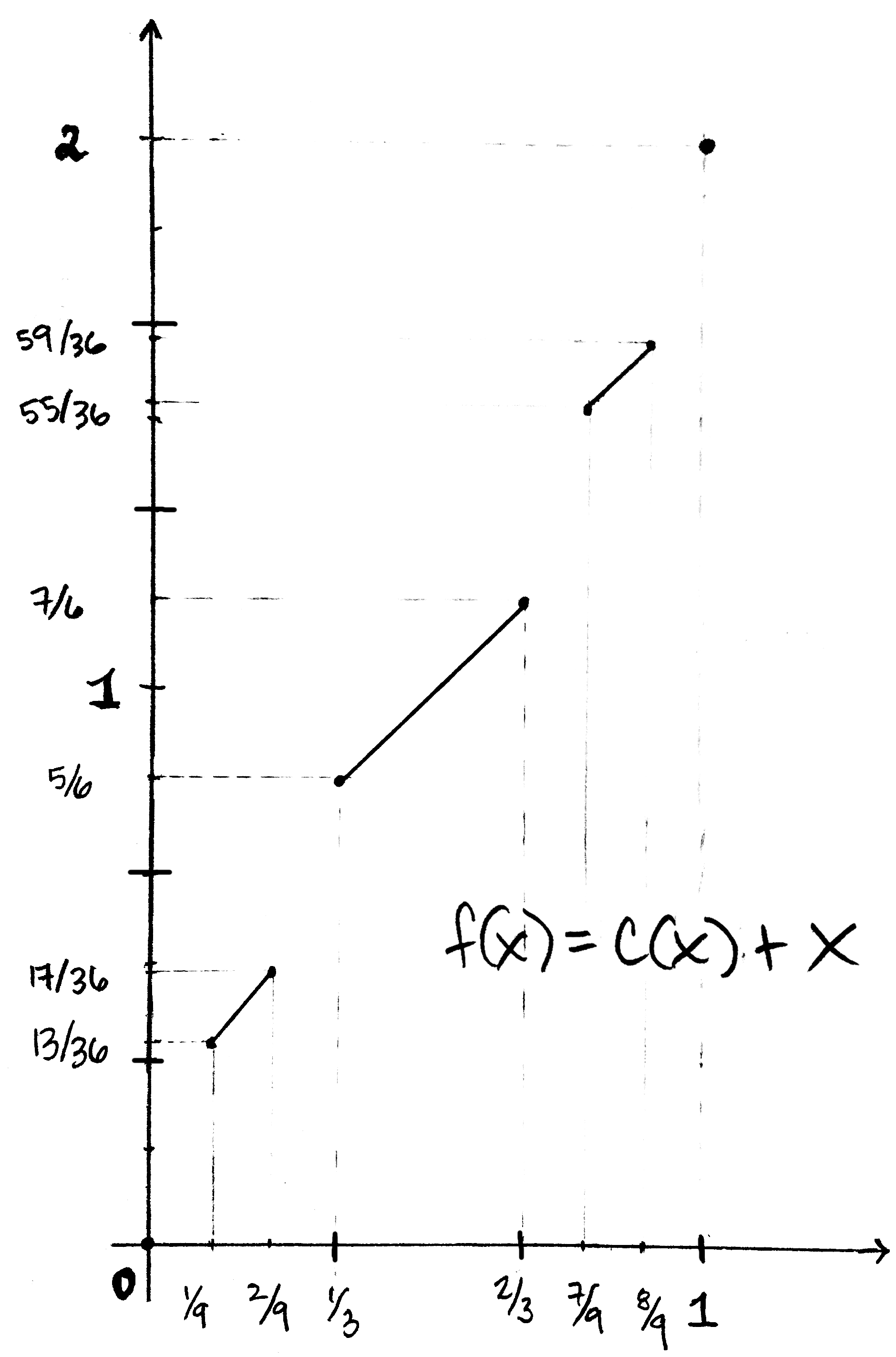
$f$ is strictly increasing
- since $f'=1$ almost everywhere (recall $c'=0$ almost everywhere)
$f$ is continuous
- since both $c$ and $x$ are continuous
$f^{-1}$ exists
- $f$ is 1-1 since it's strictly increasing; it's onto by the Intermediate Value Theorem: since $f(0)=0$, $f(1)=2$ and $f$ is continuous, it assumes all values in between $0$ and $2$!
$f^{-1}$ is continuous (hence $f$ is a homeomorphism)
- see footnote *
We should also observe that $f$ maps the intervals of $[0,1]$ which are removed during the construction of the Cantor set $\mathscr{C}$ to intervals of $[0,2]$ of the same length**. This implies $$\mu(f([0,1]\smallsetminus \mathscr{C}))=\mu([0,1]\smallsetminus \mathscr{C})=1.$$ But since $[0,2]= f(\mathscr{C})\sqcup f([0,1]\smallsetminus \mathscr{C})$, we see that $2=\mu([0,2])=\mu(f(\mathscr{C}))+\mu(f([0,1]\smallsetminus \mathscr{C}))=\mu(f(\mathscr{C}))+1$ whence $$\mu(f(\mathscr{C}))=1.$$ From this we deduce that $f(\mathscr{C})\subset[0,2]$ contains a non-measurable subset, say $N$ (see fact #1 in the introduction). And here is where we make our
Claim: $f^{-1}(N)$ is Lebesgue measurable but not Borel.
This is easy to prove, but its substance lies in the following
Lemma: A strictly increasing function defined on an interval maps Borel sets to Borel sets.
Proof of Lemma
We follow exercises #45-47 of ch. 2 in Royden's Real Analysis (4ed). Let $f$ be any strictly increasing function defined on some interval. By our analysis above, we know that such a function is a homeomorphism. This fact enables us to show that $f$ maps Borel sets to Borel sets. To do so, it suffices to show that for any continuous function $g$ the set $$\mathscr{A}=\{E:g^{-1}(E) \text{ is Borel} \}$$ is a $\sigma$-algebra containing the open sets. Once we show this, we can conclude $\mathscr{A}$ contains all the Borel sets and therefore, taking $g$ to be $f^{-1}$ (which we know is continuous!), we'll have $(f^{-1})^{-1}(E)=f(E)$ is Borel for any Borel set $E$, which is what we want.
Showing $\mathscr{A}$ is a $\sigma$-algebra (the first two bullets) which contains the open sets (the third bullet) is simple enough (recall that $\mathscr{B}$ denotes the Borel sets):
- If $\{E_i\}\subset\mathscr{A}$ then $f^{-1}(\cup E_i)=\cup f^{-1}(E_i) \in \mathscr{B}$ since $\mathscr{B}$ is a $\sigma$-algebra, hence $\cup E_i\in \mathscr{A}$.
- If $E\subset \mathscr{A}$ then $f^{-1}(E^c)=(f^{-1}(E))^c\in\mathscr{B}$ since $\mathscr{B}$ is a $\sigma$-algebra, hence $E^c\in\mathscr{A}$.
- If $U$ is open, then $f^{-1}(U)$ is open and thus an element of $\mathscr{B}$. Hence $U\in\mathscr{A}$.
We are now ready for the
Proof of Claim
Since $N\subset f(\mathscr{C})$, we know that $f^{-1}(N)\subset \mathscr{C}$ is measurable (and has measure zero) since it is a subset of a zero set and the Lebesgue measure is complete. Moreover, $f^{-1}(N)$ is not Borel! If it were, then since $f$ maps Borel sets to Borel sets by our Lemma, we'd have that $f(f^{-1}(N))=N$ is Borel. But that's impossible since $N$ isn't even measurable! This proves the claim.

Footnotes
*Proof: Let $h=f^{-1}:[0,2]\to[0,1]$ and suppose $U\subset[0,1]$ is open. Then $[0,1]\smallsetminus U$ is compact and hence closed (and bounded). Since $f$ is continuous, $f([0,1]\smallsetminus U)$ is also closed. But we can rewrite this as \begin{align*} f([0,1]\smallsetminus U)&=f([0,1])\smallsetminus f(U)\\ &=[0,2]\smallsetminus f(U)\\ &=[0,2]\smallsetminus h^{-1}(U) \end{align*} which allows us to conclude $h^{-1}(U)$ is open.
**Proof: This follows simply because $c$ is constant on any interval in $[0,1]\smallsetminus \mathscr{C}$. Indeed for any interval $(a,b)\subset[0,1]\smallsetminus\mathscr{C}$, we have $c(a)=c(b)$ and so \begin{align*} \mu((f(a),f(b)))&=f(b)-f(a)\\ &=c(b)+b-c(a)-a\\ &=b-a. \end{align*}
References
- Much of today's discussion is taken from here.
- see also Real Analysis (4ed) by Royden, section 2.7, Propositions 21 and 22
