The Fundamental Group of the Circle, Part 2

EDIT 11/22/16: I encourage the reader to skip this post and proceed directly to Part 3. Part 2 merely contains the justification of a shortcut that we never actually use in the remainder of this series. In particular, we are certainly not proving 'well-definedness,' even though that's what I claim. (Apologies, dear readers!) For more, see my explanation in the comments below. 

This week we continue our proof from Hatcher's Algebraic Topology that the fundamental group of the circle is isomorphic to $\mathbb{Z}$. Recall our outline:  

Part 1: Set-up/observations
Part 2: Show $\Phi$ is well defined
Part 3: Show $\Phi$ is a group homomorphism
Part 4: Show $\Phi$ is surjective
Part 5: Show $\Phi$ is injective  (Note: parts 4 and 5 require two lemmas whose proofs we will defer until part 5)
Part 6: Prove the two lemmas used in parts 4 and 5

Last week we defined the map $\Phi:\mathbb{Z}\to\pi_1(S^1)$ by $n\mapsto[\omega_n]$ where $\omega_n:[0,1]\to S^1$ is the loop given by $s\mapsto (\cos{2\pi ns}, \sin{2\pi ns})$. Our goal for today is to prove that $\Phi$ is well-defined, and the proof is quite simple.        

‍

Claim: Φ is Well-Defined

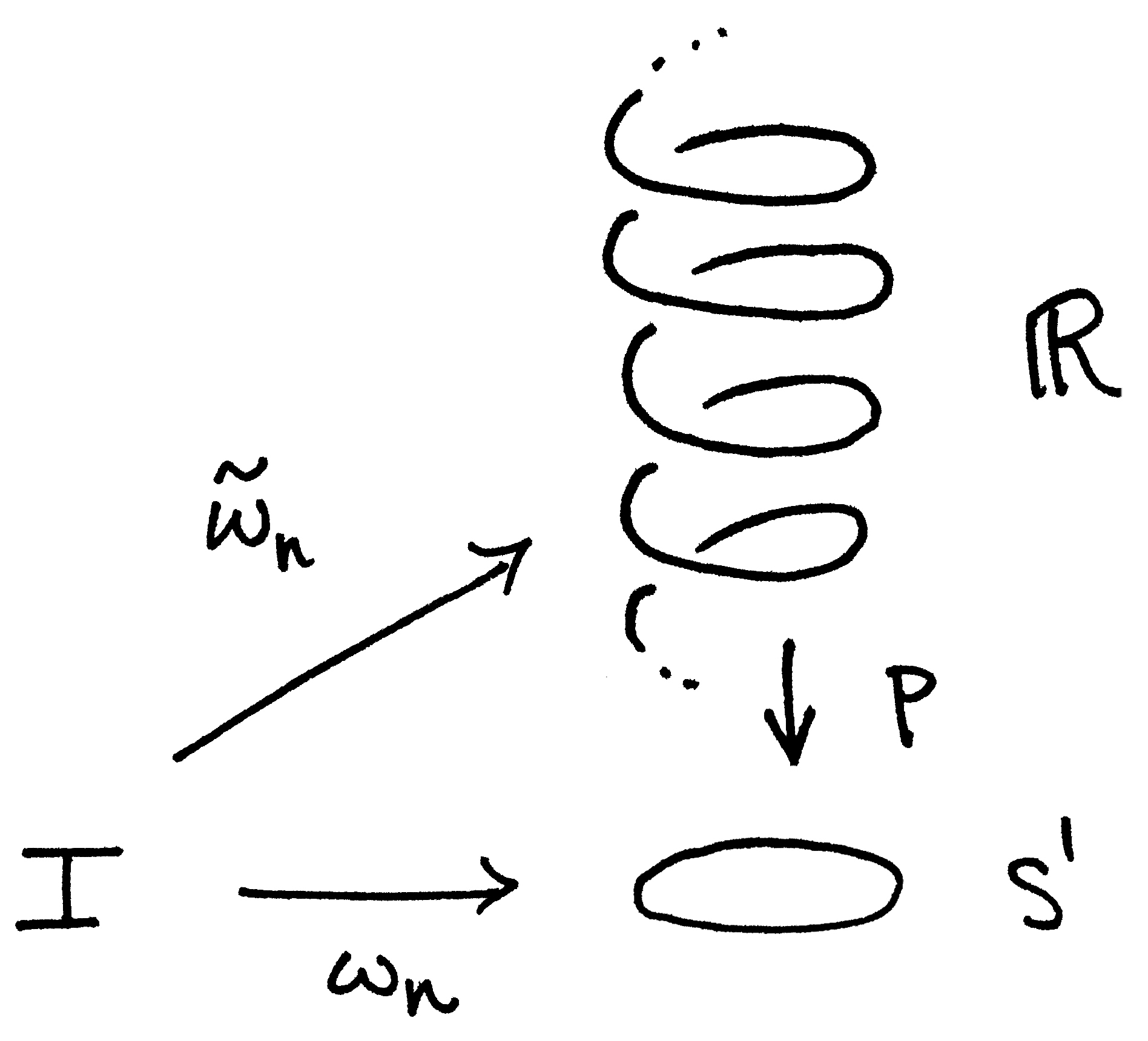
Recall that $\omega_n=p\circ\widetilde{\omega}_n$ is a loop from $I$ to $S^1$ where $\widetilde{\omega}_n:I\to\mathbb{R}$ is a path (a straight line, actually) from $0$ to $n$. We wish to show that equivalence class $[\omega_n]$ doesn't depend on its representative. In other words, we wish to show that $\omega_n$ doesn't depend on the path $\widetilde{\omega}_n$ from $0$ to $n$.

‍

To this end, let $\widetilde{\gamma}_n$ be any other path from $0$ to $n$ in $\mathbb{R}$. Then $\widetilde{\omega}_n\simeq \widetilde{\gamma}_n$ are homotopic by the straight line homotopy $F:I\times I\to\mathbb{R}$ where $F(s,t)=(1-t)\widetilde{\omega}_n+t\widetilde{\gamma}_n$.

‍

Set $\omega_n'=p\circ \widetilde{\gamma}_n$. If we can show the existence of a homotopy $G:I\times I\to S^1$ such that $$\omega_n=p\circ \widetilde{\omega}_n\;\underset{G}{\simeq}\; p\circ\widetilde{\gamma}_n=\omega_n',$$ then we'll be done since we can conclude $[\omega_n]=[\omega_n']$! But this is easy enough since we can simply let $G=p\circ F$ be the projection of the homotopy $F$ in $\mathbb{R}$ down to $S^1$:              

‍

And indeed $G$ is a homotopy since it's continuous (as both $p$ and $F$ are) and

• $G(s,0)=p(F(s,0))=p(\widetilde{\omega}_n(s))=\omega_n(s)$
• $G(s,1)=p(F(s,1))=p(\widetilde{\gamma}_n(s))=\omega_n'(s)$.

Therefore $[\omega_n]=[\omega_n']$ and so $\Phi$ is indeed well-defined.

Next time, we'll show that $\Phi$ is in fact a group homomorphism.